正常模态逻辑
编辑在逻辑学中,正常模态逻辑是一个模态公式的集合L,使得L包含。所有命题同义词;克里普克模式的所有实例:◻(A→B)→(◻A→◻B){dISPlaystyle盒子(AtoB)to(BoxAto盒子B)}。并且它是封闭的。脱离规则(moduSPonens):A→B,A∈L{displaystyleAtoB,AinL}意味着满足上述条件的最小的逻辑被称为K。大多数现在常用的模态逻辑(就有哲学动机而言),例如C.I.Lewis的S4和S5,是正常的(因此是K的扩展)。然而,一些行为逻辑和认识论逻辑,例如,是非正常的,通常是因为它们放弃了克里普克模式。每个正常的模态逻辑都是有规律的,因此也是经典的。
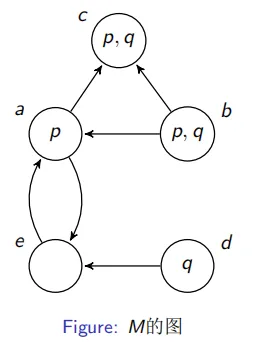
常见的正常模态逻辑
编辑下表列出了几个常见的正常模态系统。符号指的是克里普克语义学§常见模态公理模式的表格。一些系统的框架条件被简化了:就表中给出的框架类而言,这些逻辑是健全和完整的,但它们可能对应于更大的框架类。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/171302/
