寻路

寻路是指通过计算机应用程序绘制两点之间最短的路线。它是解决迷宫问题的一个更实用的变体。这一领域的研究在很大程度上是基于Dijkstra在加权图上寻找最短路径的算法。寻路与图论中的最短路径问题密切相关，后者研究如何在一个大网络中的两点之间找出最符合某些标准（最短、最便宜、最快等）的路径。

寻路方法的核心是通过从一个顶点开始，探索相邻的节点，直到到达目的节点，通常是为了找到最便宜的路线。虽然像广度优先搜索这样的图形搜索方法在有足够时间的情况下会找到一条路线，但其他探索图形的方法会倾向于更快地到达目的地。一个比喻是一个人走过一个房间；而不是事先检查每一条可能的路线，这个人一般会沿着目的地的方向走，只有在避开障碍物时才会偏离路径，并且使偏离尽可能小。寻路的两个主要问题是：（1）寻找图中两个节点之间的路径；以及（2）最短路径问题--寻找最佳最短路径。广度优先和深度优先搜索等基本算法通过穷尽所有可能性来解决xxx个问题；从给定的节点开始，它们遍历所有潜在的路径，直到到达目标节点。这些算法的运行速度为{displaystyleO(|V|+|E|)}，或线性时间，其中V是顶点数量，E是顶点之间的边数。或线性时间，其中V是顶点的数量，E是顶点之间的边的数量。更复杂的问题是寻找最优路径。这种情况下的穷举法被称为Bellman-Ford算法，它的时间复杂度为，或二次方时间。然而，没有必要检查所有可能的路径来找到最优路径。A*和Dijkstra算法等算法通过启发式方法或动态编程，战略性地消除路径。通过消除不可能的路径，这些算法的时间复杂度可以低至上述算法是xxx的一般算法之一，它们在图上操作时无需预处理。然而，在实际的旅行路线系统中，通过对图进行预处理以达到更好的性能的算法可以达到更好的时间复杂度。这样的算法之一是收缩层次结构。

基于图的寻路算法的一个常见例子是Dijkstra算法。这个算法从一个起始节点和一个开放的候选节点集开始。在每个步骤中，开放集中与起点距离最小的节点被检查。该节点被标记为关闭，与之相邻的所有节点如果尚未被检查，则被添加到开放集。这个过程重复进行，直到找到通往目的地的路径。由于最低距离的节点首先被检查，所以xxx次发现目的地时，通向它的路径将是最短的路径。如果有一个负的边缘权重，Dijkstra的算法就会失败。在假设的情况下，节点A、B、C组成一个连接的无向图，边AB=3，AC=4，BC=-2，从A到C的最优路径花费1，从A到B的最优路径花费2。Dijkstra算法从A开始将首先检查B，因为它是最近的。它将给它分配一个3的成本，并将其标记为关闭，这意味着它的成本将永远不会被重新评估。因此，Dijkstra的方法不能评估负的边权重。然而，由于在许多实际应用中，永远不会出现负的边权重，Dijkstra的算法在很大程度上适合寻路的目的。

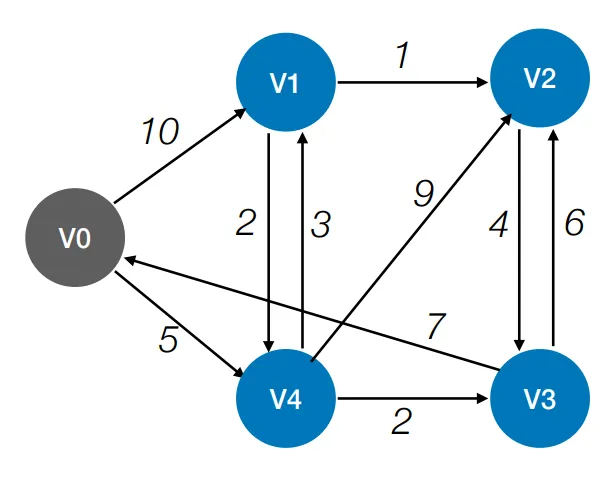
A*算法A*是Dijkstra算法的一个变种，常用于游戏中。A*给每个开放节点分配一个权重，等于通往该节点的边的权重加上该节点与终点之间的近似距离。这个近似距离是由启发式算法找到的，代表了该节点与终点之间的最小可能距离。这使得它能够在找到初始路径后消除更长的路径。如果在起点和终点之间有一条长度为x的路径，而一个节点和终点之间的最小距离大于x，那么这个节点就不需要被检查。