超参数优化

在机器学习中，超参数优化或调整是为学习算法选择一组最佳的超参数的问题。超参数是一个参数，其值被用来控制学习过程。相比之下，其他参数（通常是节点权重）的值是学习的。同一种机器学习模型可能需要不同的约束条件、权重或学习率来概括不同的数据模式。这些措施被称为超参数，必须进行调整，以便模型能够最佳地解决机器学习问题。超参数优化找到一个超参数的元组，产生一个最佳的模型，使给定的独立数据上的预定损失函数最小。目标函数采用一个超参数的元组，并返回相关的损失。交叉验证通常被用来估计这种泛化性能。

执行超参数优化的传统方法是网格搜索或参数扫描，这只是在学习算法的超参数空间的手动指定子集中进行详尽的搜索。网格搜索算法必须由一些性能指标来指导，通常由训练集上的交叉验证或保留验证集上的评估来衡量。由于机器学习者的参数空间可能包括某些参数的实值或无界值空间，在应用网格搜索之前，可能需要手动设置界限和离散化。例如，一个典型的配有RBF核的软边缘SVM分类器至少有两个超参数需要调整，以便在未见过的数据上有好的表现：正则化常数C和核超参数γ。然后，网格搜索用这两个集合的笛卡尔积中的每一对（C，γ）训练一个SVM，并在一个保留的验证集上评估它们的性能（或者通过训练集的内部交叉验证，在这种情况下，每对SVM被训练多个）。最后，网格搜索算法输出在验证程序中获得最高分的设置。网格搜索受到维度诅咒的影响，但由于它所评估的超参数设置通常是相互独立的，所以往往是令人尴尬的平行。

随机搜索通过随机选择取代了对所有组合的详尽列举。这可以简单地应用于上述的离散设置，但也可以推广到连续和混合空间。它可以胜过网格搜索，特别是当只有少量的超参数影响到机器学习算法的最终性能。在这种情况下，据说优化问题的内在维度很低。随机搜索也是令人尴尬的并行，另外还允许通过指定取样的分布来纳入先验知识。尽管它很简单，但随机搜索仍然是比较新的超参数优化方法性能的重要基准线之一。

贝叶斯优化是一种针对噪声黑箱函数的全局优化方法。应用于超参数优化，贝叶斯优化建立了一个从超参数值到目标的函数映射的概率模型，在验证集上评估。通过反复评估基于当前模型的有希望的超参数配置，然后对其进行更新，贝叶斯优化的目的是收集观察结果，揭示关于该函数的尽可能多的信息，特别是最佳位置。

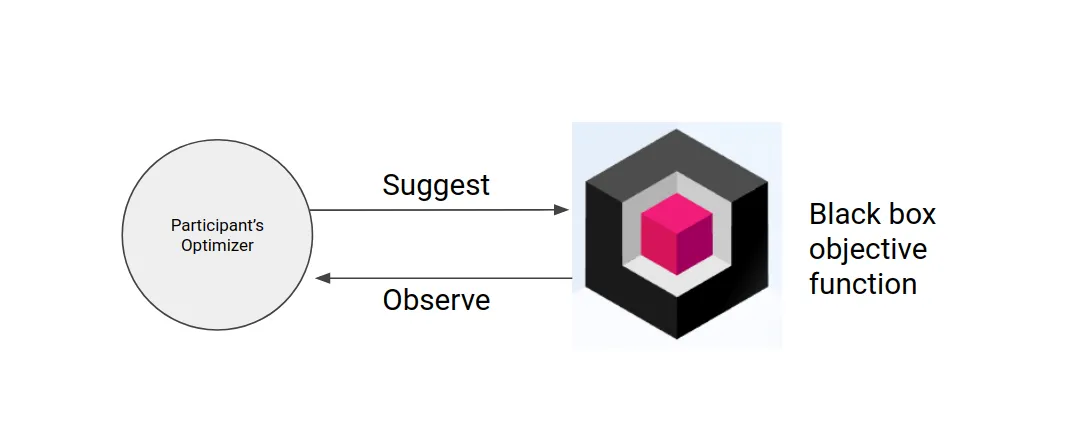
它试图平衡探索（结果最不确定的超参数）和利用（预期接近最优的超参数）。在实践中，贝叶斯优化已被证明与网格搜索和随机搜索相比，能在较少的评估中获得更好的结果，这是因为它能够在实验运行前对实验的质量进行推理。

对于特定的学习算法，可以计算相对于超参数的梯度，然后用梯度下降法优化超参数。这些技术的首次使用集中在神经网络上。此后，这些方法被扩展到其他模型，如支持向量机或逻辑回归。为了获得与超参数有关的梯度，一种不同的方法包括使用自动微分来区分迭代优化算法的步骤。沿着这个方向，最近的一项工作是使用im