解析信号

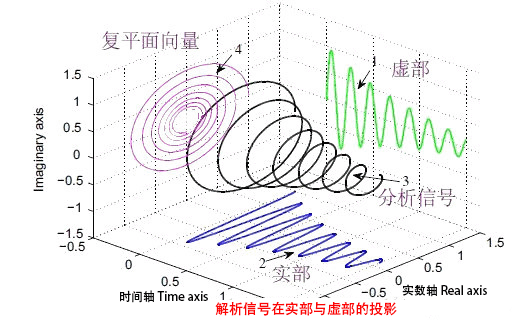
在数学和信号处理中，解析信号是一个没有负频率成分的复值函数。 解析信号的实部和虚部是通过希尔伯特变换相互关联的实值函数。

一个实值函数的解析表示是一个解析信号，包括原始函数和它的希尔伯特变换。这种表示方法有利于许多数学操作。其基本思想是，实值函数的傅里叶变换（或频谱）的负频率成分是多余的，因为这样的频谱具有赫米特对称性。只要愿意处理复值函数，这些负的频率成分可以被丢弃而不损失任何信息。这使得函数的某些属性更容易获得，并促进了调制和解调技术的推导，如单边带。

只要被操纵的函数没有负的频率成分（也就是说，它仍然是解析的），从复数到实数的转换只是一个抛弃虚数部分的问题。解析表示法是相位概念的概括：相位被限制在时间不变的振幅、相位和频率上，而解析信号则允许时间可变的参数。

如果s ( t ) {displaystyle s(t)}是一个具有傅里叶变换S ( f ) {displaystyle S(f)}的实值函数，那么该变换对f = 0 {displaystyle f=0}轴具有赫米特对称性。

• [s(t)]}是s ( t ) {displaystyle s(t)}的希尔伯特变换；
• ∗ {displaystyle *}是二元卷积算子；
• j {displaystyle j}是虚单位。

这也可以表示为一种直接去除负频率成分的过滤操作。