在数学中（特别是在复数分析中），复数z的参数，表示为arg(z)，是正实轴与连接原点和z的线之间的角度，表示为复平面中的一个点，在图1中表示为φ {dISPlaystylevarphi }。它是一个在非零复数上操作的多值函数。为了定义一个单值函数，使用参数的主值（有时表示为Arg z）。它通常被选择为位于区间（-π，π）内的唯一参数值。

复数的一个参数z = x + iy，表示为arg(z)，以两种等价方式定义：

• 几何上，在复平面内，作为从正实轴到代表z的矢量的二维极角φ {diSPlaystylevarphi } 。数值由角度给出，单位是弧度，如果逆时针测量，则为正数。
• 代数上，作为任何实数φ {displaystyle varphi }，
• 对于模数来说，幅度这个名字和对于参数来说，相位这个名字有时被等同使用。

在这两个定义下，可以看到任何非零复数的参数都有许多可能的值：首先，作为一个几何角度，很明显整个圆的旋转不会改变点，所以相差2π弧度的整数倍（一个完整的圆）的角度是相同的，同样地，从sin和cos的周期性来看，第二个定义也有这个特性。零的参数通常不作定义。

复数参数也可以用复数根的代数方法定义,这个定义消除了对其他难以计算的函数的依赖，如正切，也消除了对分片定义的需要。因为它是以根为单位定义的，所以它也继承了平方根的主枝作为自己的主枝。通过除以 | z | {displaystyle |z|}对z进行归一化并不是收敛到正确值所必需的，但它确实加快了收敛速度，并确保arg ( 0 ) {displaystyle arg(0)}不被定义。

因为围绕原点的完全旋转会使一个复数保持不变，所以有很多选择可以通过绕过原点的任何次数对φ {displaystylevarphi }作出选择。是多值（集值）函数f ( x , y ) = arg ( x + i y ) {displaystyle f(x,y)=arg(x+iy)}的表示，其中一条垂直线（图中未显示）在代表该点所有可能的角度选择的高度上切割表面。

当需要一个定义明确的函数时，那么通常的选择，即所谓的主值，是在开闭区间(-π rad, π rad)的值，即从-π到π弧度，不包括-π弧度本身（相当于从-180到+180度，不包括-180°本身）。这代表了从正实轴任何一个方向上最多半个完整圆的角度。

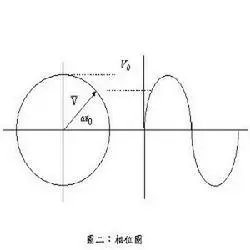
一些作者将主值的范围定义为在闭合-开放区间内。

许多文章说，该值由arctan(y/x)给出，因为y/x是斜率，而arctan将斜率转换为角度。这只有在x > 0时才是正确的，所以商被定义了，角度位于-π/2和π/2之间，但是将这个定义扩展到x不是正数的情况下就比较麻烦了。具体来说，我们可以在两个半平面x > 0和x < 0（如果希望在负x轴上进行分支切割，则分成两个象限）上分别定义参数的主值，y > 0，y < 0，然后一起修补。