狄拉克符号
编辑假设在 V {dISPlaystyle V} 上存在一个内积 ( ⋅ , ⋅ ) {diSPlaystyle (cdot ,cdot )} 具有反线性第一个参数,这使得 V {displaystyle V} 是一个内积 产品空间。 然后用这个内积每个向量 ϕ ≡ | ϕ ⟩ {displaystyle {boldsymbol {phi }}equiv |phi rangle } 可以用相应的线性形式来识别,方法是将向量放在内部的反线性第一个槽中
对于向量空间 C n {displaystyle mathbb {C} {n}} ,可以用列向量识别 kets,用行向量识别 bras。 bras、kets 和线性运算符的组合使用矩阵乘法进行解释。
特别是,当还使用行和列向量标识时,具有相同标签的 kets 和 bras 使用 Hermitian 共轭列和行向量标识。
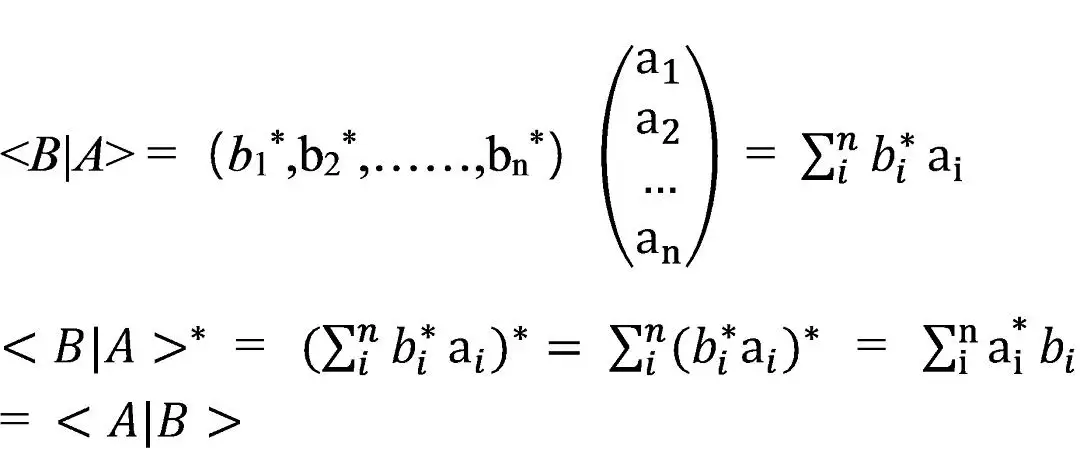
简介
编辑狄拉克符号是复向量空间及其对偶空间有限维和无限维情况下线性代数和线性算子的符号。 它专门设计用于简化量子力学中经常出现的计算类型。 它在量子力学中的应用相当广泛。 许多使用量子力学解释的现象都使用括号符号来解释。
向量空间
编辑向量 vs kets
编辑在数学中,术语向量用于任何向量空间的元素。 然而,在物理学中,矢量这个术语更为具体:矢量几乎专门指位移或速度等量,它们的分量直接与空间的三个维度相关,或者相对论地与时空的四个维度相关。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/193664/
