平面应力

在连续介质力学中，如果特定平面上的应力矢量为零，则称材料处于平面应力之下。 当这种情况发生在结构的整个元素上时，就像薄板的情况一样，应力分析会xxx简化，因为应力状态可以用 2 维张量表示（可以表示为 2×2 矩阵而不是 大于 3×3)。 一个相关的概念，平面应变，通常适用于非常厚的构件。

平面应力通常发生在薄平板中，这些平板仅受与其平行的载荷力作用。 在某些情况下，出于应力分析的目的，也可以假定弯曲较缓的薄板具有平面应力。 例如，充满压力流体的薄壁圆筒就是这种情况。 在这种情况下，与平行于板的应力分量相比，垂直于板的应力分量可以忽略不计。

然而，在其他情况下，薄板的弯曲应力不能忽略。 人们仍然可以通过使用二维域来简化分析，但每个点的平面应力张量必须用弯曲项补充。

从数学上讲，如果三个主应力之一（柯西应力张量的特征值）为零，则材料中某点的应力为平面应力。

例如，考虑沿 x {\displaystyle x} 、y {\displaystyle y} 和 z {\displaystyle z} 测量 10、40 和 5 厘米的矩形材料块，它在 x 方向上被拉伸 {\displaystyle x} 方向并在 y {\displaystyle y} 方向上压缩，由一对大小分别为 10 N 和 20 N 的相反力均匀分布在相应的面上。

更一般地，如果任意选择前两个坐标轴但垂直于零应力方向

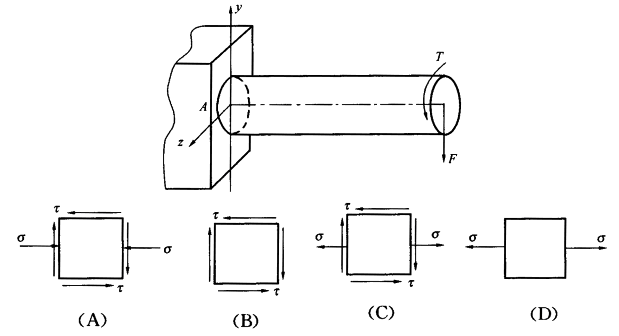
在某些情况下，平面应力模型可用于分析缓曲面。 例如，考虑一个薄壁圆柱体承受沿其边缘均匀分布的轴向压缩载荷，并充满加压流体。 内部压力将在壁上产生反作用环向应力，即垂直于圆柱轴并与其表面相切的法向拉伸应力。 圆柱体可以在概念上展开并分析为一个扁平的薄矩形板，在一个方向上承受拉伸载荷，在另一个方向上承受压缩载荷，两个方向都平行于板。

如果一个维度与其他维度相比非常大，则最长维度方向上的主应变受到约束并且可以假定为常数，这意味着沿该方向的应变实际上为零，因此产生平面应变条件（图 7.2） ). 在这种情况下，尽管所有主应力都不为零，但计算时可以忽略最长尺寸方向的主应力。 因此，允许对应力进行二维分析，例如 在水库加载的横截面上分析的大坝。