算术下溢
编辑术语算术下溢(也称为浮点下溢,或简称下溢)是计算机程序中的一种情况,其中计算结果是比计算机在其中央处理单元(CPU)的内存中实际表示的更精确的绝对值 ).
当浮点运算的真实结果在数量级上小于(即接近于零)小于目标数据类型中可表示为普通浮点数的最小值时,可能会发生计算下溢。 下溢可以部分地视为浮点值的指数的负溢出。 例如,如果指数部分可以表示从-128 到127 的值,那么小于-128 的结果可能会导致下溢。
在整数变量中存储太低的值(例如,尝试将 −1 存储在无符号整数中)被恰当地称为整数溢出,或更广泛地称为整数回绕。 术语下溢通常仅指浮点数,这是一个单独的问题。 在大多数浮点设计中不可能存储太低的值,因为通常它们是有符号的并且具有负无穷大值。
下溢间隙
编辑−fminN 和 fminN 之间的间隔,其中 fminN 是最小正正常浮点值,称为下溢间隙。 这是因为这个区间的大小比间隙外的相邻正常浮点值之间的距离大很多数量级。 例如,如果浮点数据类型可以表示 20 位,则下溢间隙比间隙外相邻浮点值之间的绝对距离大 221 倍。
在旧设计中,下溢间隙只有一个可用值,即零。 当发生下溢时,真实结果被零替换(直接由硬件替换,或由处理主要下溢条件的系统软件替换)。 这种替换称为清零。
1984 年版的 IEEE 754 引入了次正规数。 次正规数(包括零)用值填充下溢间隙,其中相邻值之间的绝对距离与下溢间隙外的相邻值的绝对距离相同。 这会启用逐渐下溢,其中使用最接近的次正常值,就像尽可能使用最接近的正常值一样。 即使在使用逐渐下溢时,最接近的值也可能为零。
刚好在间隙之外的相邻浮点值之间的绝对距离称为机器 epsilon,通常以最大值为特征,其与值 1 的总和将导致该浮点方案中值为 1 的答案。 这可以写成 fl ( 1 + ϵ ) = 1 {dISPlaystyle fl(1+epsilon )=1} ,其中 fl ( ) {diSPlaystyle fl()} 是一个函数,它将实数值转换为 浮点表示法。 虽然不要将机器 epsilon 与下溢水平(假设次正规数)混淆,但它密切相关。 机器 epsilon 取决于构成有效数字的位数,而下溢级别取决于构成指数字段的位数。 在大多数浮点系统中,下溢水平小于机器 epsilon。
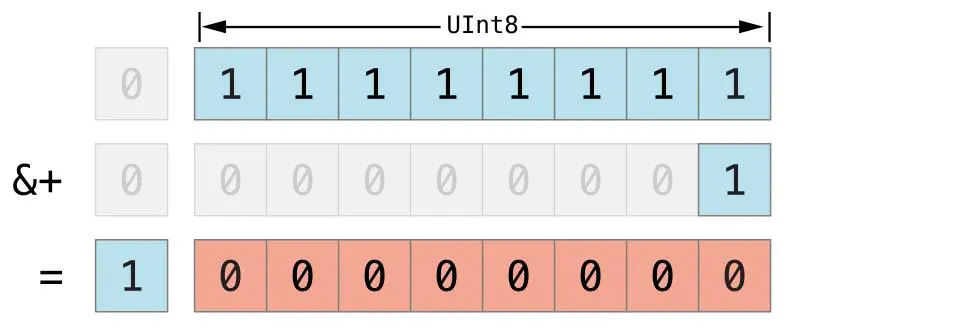
下溢的处理
编辑下溢的发生可能会设置(粘性)状态位、引发异常、在硬件级别生成中断,或者可能导致这些影响的某种组合。
按照 IEEE 754 的规定,下溢条件仅在精度损失时才发出信号。 通常这被确定为最终结果不准确。但是,如果用户陷入下溢,则无论是否考虑精度损失,这都可能发生。 IEEE 754 中对下溢(以及其他异常)的默认处理是将已发生的下溢记录为浮点状态。 这是为应用程序编程级别指定的,但通常也被解释为如何在硬件级别处理它。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/195891/
