拓扑绝缘体

拓扑绝缘体是一种材料，其内部表现为电绝缘体，而其表面表现为电导体，这意味着电子只能沿着材料的表面移动。

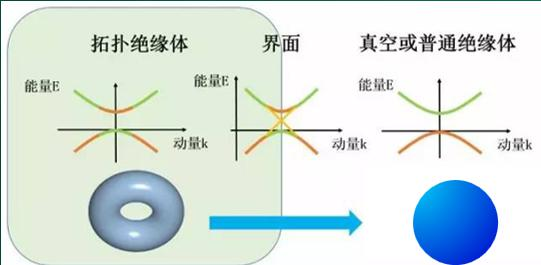
拓扑绝缘体是绝缘体，原因与普通（普通）绝缘体相同：材料的价带和导带之间存在能隙。 但在拓扑绝缘体中，这些带在非正式意义上是扭曲的，相对于一个普通的绝缘体。 拓扑绝缘体不能在不解开能带的情况下连续转变为普通绝缘体，这会关闭带隙并产生导电状态。 因此，由于底层场的连续性，拓扑绝缘体与平凡绝缘体（包括拓扑平凡的真空）的边界被迫支持导电状态。

由于这是拓扑绝缘体带结构的全局特性的结果，因此局部（保持对称性）扰动不会破坏该表面状态。 这是拓扑绝缘体所独有的：虽然普通绝缘体也可以支持导电表面态，但只有拓扑绝缘体的表面态具有这种鲁棒性。

这导致了拓扑绝缘体的更正式的定义：如果不通过中间导电状态就不能绝热地转变为普通绝缘体的绝缘体。 换句话说，拓扑绝缘体和普通绝缘体是相图中的独立区域，仅通过导电相连接。 通过这种方式，拓扑绝缘体提供了一种物质状态的示例，该物质状态未被定义普通物质状态的 Landau 对称性破缺理论所描述。

拓扑绝缘体的特性及其表面状态在很大程度上取决于材料的尺寸及其基本对称性，并且可以使用所谓的拓扑绝缘体周期表进行分类。 维度和对称性的某些组合完全禁止拓扑绝缘体。 所有拓扑绝缘体都至少具有粒子数守恒的 U(1) 对称性，并且通常由于没有磁场而具有时间反转对称性。 这样，拓扑绝缘体就是对称保护拓扑序的一个例子。 所谓的拓扑不变量，在 Z 2 {displaystyle mathbb {Z} _{2}} 或 Z {displaystyle mathbb {Z} } 中取值，允许将绝缘体分类为平凡的或拓扑的，并且 可以通过各种方法计算。

拓扑绝缘体的表面状态可能具有奇特的特性。 例如，在时间反转对称 3D 拓扑绝缘体中，表面态的自旋锁定在与其动量成直角的位置（自旋动量锁定）。 在给定的能量下，仅有的其他可用电子态具有不同的自旋，因此 U 形转弯散射受到强烈抑制，表面上的传导具有高度金属性。

尽管它们起源于量子力学系统，但拓扑绝缘体的类似物也可以在经典介质中找到。 存在光子、磁和声学拓扑绝缘体等。

xxx个 3D 拓扑绝缘体模型由 Volkov 和 Pankratov 于 1985 年提出，随后由 Pankratov、Pakhomov 和 Volkov 于 1987 年提出。PbTe/SnTe 和 HgTe/CdTe 异质结构中的能带反转接触处显示存在无间隙二维狄拉克态 . 2007 年，Molenkamp 小组在二维拓扑绝缘体中通过实验验证了 HgTe/CdTe 中界面狄拉克态的存在。

Kane 和 Mele 于 2005 年以及 Bernevig 和 Zhang 于 2006 年提出了二维拓扑绝缘体（也称为量子自旋霍尔绝缘体）的后期理论模型集。 Z 2 {displaystyle mathbb {Z } _{2}} 拓扑不变量被构建，时间反转对称性的重要性在 Kane 和 Mele 的工作中得到阐明。 随后，Bernevig、Hughes 和 Zhang 做出理论预测，具有一维 (1D) 螺旋边缘态的 2D 拓扑绝缘体将在夹在碲化镉之间的碲化汞量子阱（非常薄的层）中实现。 在 2007 年 Molenkamp 小组的实验中确实观察到了由于 1D 螺旋边缘状态引起的传输。

尽管在 2000 年代就指出了拓扑分类和时间反演对称性的重要性，但在 80 年代的著作中已经了解了拓扑绝缘体的所有必要成分和物理学。

2007 年，有人预测可能会在涉及铋的二元化合物中发现 3D 拓扑绝缘体，特别是存在无法还原为量子自旋霍尔态的多个副本的强拓扑绝缘体。

二维拓朴绝缘体首先在包含夹在镉 t 之间的 HgTe 量子阱的系统中实现。