格雷码

反射二进制码 (RBC)，也称为反射二进制 (RB) 或弗兰克·格雷 (Frank Gray) 之后的格雷码，是二进制数字系统的一种排序方式，使得两个连续值仅相差一位（二进制数字）。

例如，十进制值 1 在二进制中的表示通常为 001，2 为 010。在格雷码中，这些值表示为 001 和 011。这样，将一个值从 1 递增到 2 只需要一位 改变，而不是两个。

格雷码广泛用于防止机电开关的杂散输出，以及促进数字通信（例如数字地面电视和某些有线电视系统）中的纠错。

许多设备通过关闭和打开开关来指示位置。 如果该设备使用自然二进制代码，则位置 3 和 4 彼此相邻，但二进制表示的所有三位都不同：

自然二进制代码的问题在于物理开关并不理想：物理开关不太可能完全同步地改变状态。 在上面显示的两个状态之间的转换中，所有三个开关都会改变状态。 在所有都在变化的短暂时间内，开关会读取一些虚假位置。 即使没有按键弹跳，转换也可能看起来像 011 — 001 — 101 — 100。当开关出现在位置 001 时，观察者无法判断这是真正的位置 1，还是其他两个位置之间的过渡状态。 如果输出可能通过组合逻辑馈入顺序系统，则顺序系统可能会存储错误值。

这个问题可以通过一次只改变一个开关来解决，所以位置永远不会有任何歧义，导致代码分配给一组连续的整数中的每一个，或者分配给循环列表的每个成员，一个符号的单词，例如 没有两个码字是相同的，并且每两个相邻的码字恰好相差一个符号。 这些代码也称为单位距离、单距离、单步、单调或同步代码，参照相邻代码之间的汉明距离 1。

原则上，对于给定的字长，可以有多个这样的代码，但术语格雷码首先应用于非负整数的特定二进制代码，二进制反射格雷码或 BRGC。 贝尔实验室研究员 George R. Stibitz 在 1941 年的专利申请中描述了这样一种代码，该申请于 1943 年获得批准。Frank Gray 在他 1947 年的专利申请中引入了反射二进制代码一词，并指出该代码当时还没有公认的名称。 他的名字来源于这样一个事实，即它可以通过一种反射过程从传统的二进制代码中构建出来。

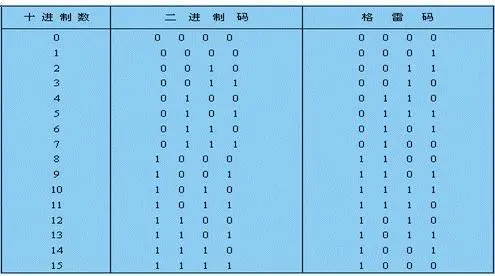
在标准编码中，最低有效位遵循 2 开，2 关的重复模式 ( … 11001100 … )； 下一个数字是 4 开，4 关的模式； 第 n 个最低有效位是 2n on 2n off 的模式。 它的四位版本如下所示：

对于十进制 15，代码只需更改一个开关就翻转到十进制 0。 这称为代码的循环或邻接属性。

在现代数字通信中，格雷码起着重要的纠错作用。 例如，在 QAM 等数字调制方案中，数据通常以 4 位或更多位的符号传输，信号的星座图被安排为使得相邻星座点传送的位模式仅相差一位。 通过将其与能够纠正单个比特错误的前向纠错相结合，接收器可以纠正任何导致星座点偏离到相邻点区域的传输错误。 这使得传输系统不易受噪声影响。

尽管 Stibitz 在 Gray 之前描述了这个代码，但反射的二进制代码后来被其他使用它的人以 Gray 命名。 1953 年的两个不同的专利申请使用格雷码作为反射二进制代码的替代名称； 其中之一还列出了名称中的最小错误代码和循环排列代码。 1954 年的一项专利申请涉及贝尔电话格雷码。 其他名称包括循环二进制代码、循环递增代码、循环置换二进制或循环置换二进制 (CPB)。

格雷码有时被错误地归因于 Elisha Gray。

反射二进制代码在被工程师所知之前就被应用于数学难题。

二进制反射的格雷码代表了中国古典圆环拼图的基本方案，这是一种由法国路易斯格罗斯于 1872 年描述的顺序机械拼图机制。

它可以作为河内塔问题的解决指南，该问题基于法国人 Édouard Lucas 在 1883 年的游戏。类似地，所谓的布加勒斯特塔和克拉根福塔游戏配置产生三元和五元格雷码。