P/NP问题

如果一个问题的解决方案很容易检查正确性，那么这个问题就一定很容易解决吗？

（计算机科学中更多未解决的问题）

P/NP问题是理论计算机科学中一个主要未解决的问题。 用通俗的话说，它问的是每一个可以快速验证解决方案的问题是否也可以快速解决。

上面使用的非正式术语 quickly 表示存在解决在多项式时间内运行的任务的算法，使得完成任务的时间随着算法输入大小的多项式函数而变化（相对于， 比方说，指数时间）。 一些算法可以在多项式时间内提供答案的一般问题类别是 P 或 P 类。对于某些问题，没有已知的方法可以快速找到答案，但是如果提供了显示答案的信息， 可以快速验证答案。 可以在多项式时间内验证答案的问题类别是 NP，它代表非确定性多项式时间。

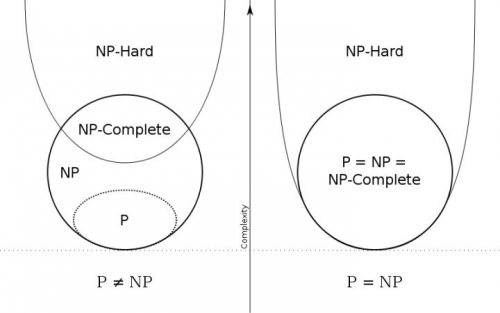
P 与 NP 问题的答案将决定可以在多项式时间内验证的问题是否也可以在多项式时间内解决。 如果事实证明 P ≠ NP（人们普遍认为），则意味着 NP 中存在计算比验证更难的问题：它们无法在多项式时间内解决，但答案可以在多项式时间内验证 .

该问题被称为计算机科学中最重要的开放问题。 除了是计算理论中的一个重要问题之外，任何一种证明都将对数学、密码学、算法研究、人工智能、博弈论、多媒体处理、哲学、经济学和许多其他领域产生深远的影响。

它是克莱数学研究所选出的七个千年奖问题之一，每个问题的第一个正确解决方案都有 1,000,000 美元的奖金。

以数独为例，这是一种游戏，玩家将获得部分填满的数字网格，并尝试按照特定规则完成网格。 给定一个不完整的数独网格，无论大小，是否至少有一个合法的解决方案？ 任何建议的解决方案都很容易验证，并且随着网格变大，检查解决方案的时间会缓慢（多项式）增长。 然而，对于困难的例子，所有已知的寻找解决方案的算法都需要随着网格变大而呈指数增长的时间。 因此，数独属于 NP（可快速检查）但似乎不属于 P（可快速求解）。 数以千计的其他问题看起来很相似，因为它们检查起来很快，但解决起来却很慢。 研究人员已经表明，NP 中的许多问题都具有额外的属性，即对其中任何一个问题的快速解决方案都可以用来构建对 NP 中任何其他问题的快速解决方案，这种属性称为 NP 完备性。 几十年的探索都没有找到解决这些问题的快速方法，因此大多数科学家怀疑这些问题都无法快速解决。 然而，这一点从未得到证实。

P/NP 问题的精确陈述于 1971 年由 Stephen Cook 在其开创性论文 The complexity of theorem proving procedures 中引入（并由 Leonid Levin 在 1973 年独立发表）。

虽然 P/NP 问题是在 1971 年正式定义的，但之前对所涉及的问题、证明的难度以及潜在的后果都有一些暗示。 1955 年，数学家约翰·纳什 (John Nash) 给美国国家安全局 (NSA) 写了一封信，他在信中推测破解足够复杂的代码需要的时间与密钥长度成指数关系。 如果得到证明（纳什对此持适当的怀疑态度），这将意味着现在所谓的 P ≠ NP，因为提议的密钥可以很容易地在多项式时间内得到验证。 库尔特·哥德尔 (Kurt Gödel) 1956 年写给约翰·冯·诺依曼 (John von Neumann) 的一封信中再次提到了潜在的问题。 哥德尔询问定理证明（现在已知是 co-NP-complete）是否可以在二次或线性时间内解决，并指出了最重要的结果之一——如果是这样，那么数学证明的发现就可以自动化。

复杂性类 P 和 NP 之间的关系在计算复杂性理论中进行了研究，计算理论的一部分处理计算期间解决给定问题所需的资源。 最常见的资源是时间（解决一个问题需要多少步）和空间（解决一个问题需要多少内存）。

在此类分析中，需要分析时间的计算机模型。 通常，此类模型假设计算机是确定性的（给定计算机的当前状态和任何输入，计算机可能只采取一种可能的操作）和顺序的（它一个接一个地执行操作）。

在这个理论中，P 类包含所有那些可以在确定性顺序机器上以 t 的数量解决的决策问题。