哥德尔数

在数理逻辑中，哥德数是一种函数，它为某些形式语言的每个符号和格式正确的公式分配一个xxx的自然数，称为哥德尔数。 这个概念是由库尔特·哥德尔为证明他的不完备性定理而提出的。

哥德数字可以解释为一种编码，其中将一个数字分配给数学符号的每个符号，之后自然数序列可以表示符号序列。 这些自然数序列可以再次由单个自然数表示，便于它们在形式算术理论中的操作。

自 1931 年哥德尔论文发表以来，哥德尔数或哥德尔代码一词已被用来指代自然数对数学对象的更一般分配。

哥德尔指出，系统中的每个陈述都可以用一个自然数（它的哥德尔数）来表示。 这一点的意义在于，一个陈述的属性——比如它的真或假——等同于确定它的哥德尔数是否具有某些属性。 涉及的人数可能确实很多，但这不是障碍； 重要的是可以构建这样的数字。

简单来说，他设计了一种方法，通过这种方法，系统中可以制定的每一个公式或陈述都得到一个xxx的数字，这样公式和哥德尔数就可以机械地来回转换。 有很多方法可以做到这一点。 一个简单的例子是在计算机中使用 ASCII 将英语存储为数字序列的方式。 由于 ASCII 代码在 0 到 127 范围内，因此将它们填充为 3 个十进制数字然后将它们连接起来就足够了：

• foxy 这个词用 102111120121 表示。
• 逻辑公式 x=y => y=x 表示为 120061121032061062032121061120。

哥德尔使用了一个基于质因数分解的系统。 他首先为他所处理的算术形式语言中的每个基本符号分配了一个xxx的自然数。

为了对整个公式（即一系列符号）进行编码，哥德尔使用了以下系统。

根据算术基本定理，任何数（尤其是用这种方法得到的数）都可以xxx地因式分解为质因数，因此可以从其哥德尔数（对于任何给定数 n 要编码的符号）。

哥德尔特别在两个层面上使用了这个方案：首先，对代表公式的符号序列进行编码，其次，对代表证明的公式序列进行编码。 这使他能够显示关于自然数的陈述与关于自然数定理可证明性的陈述之间的对应关系，这是证明的关键观察。 （哥德尔 1931）

有更复杂（也更简洁）的方法来构造序列的哥德数。

内格尔和纽曼使用的具体哥德数中，符号0的哥德尔数为6，符号=的哥德尔数为5。因此，在他们的体系中，公式0 = 0的哥德尔数为26 × 35 × 56 = 243,000,000。

无限多个不同的哥德数是可能的。 例如，假设有 K 个基本符号，可以通过将这组符号可逆映射（例如，通过可逆函数 h）到双射基 K 数字系统的数字集来构造替代哥德数。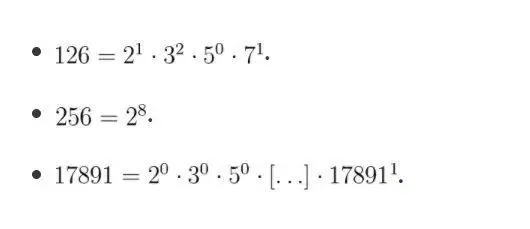

换句话说，通过以某种固定顺序放置 K 个基本符号集，使得第 i {displaystyle i} 个符号xxx对应于第 i {displaystyle i} 个双射基 K 的数字 数字系统，每个公式都可以作为它自己的哥德尔数的数字。

例如这里描述的编号有K=1000。

可以使用哥德数来说明值过程递归定义的函数实际上是原始递归函数。