达西–威斯巴哈方程式
编辑在流体动力学中,达西-威斯巴哈方程式是一个经验方程式,它将水头损失或压力损失联系起来,由于沿给定长度的管道的摩擦与不可压缩流体的流体流动的平均速度有关。
达西-威斯巴哈方程序包含一个无量纲摩擦系数,称为达西摩擦系数。
压力损失方程
编辑在直径为 D 且充满液体的圆柱形管道中,粘性效应导致的压力损失 Δp 与长度 L 成正比,可以用达西-威斯巴哈方程序式表示
其中每单位长度的压力损失 Δp/L(SI 单位:Pa/m)是以下函数的函数:
ρ,流体的密度(kg/m3);D H ,管道的水力直径,平均流速,通过实验测量为体积流量 每单位截面积润湿面积的速率 Q (m/s);f D ,达西摩擦系数。
对于直径为 D c 的圆管中的层流,摩擦因数与雷诺数成反比 (fD = 64/Re),雷诺数本身可以用容易测量的或 公布的物理量。
μ为流体的动力粘度(Pa·s=N·s/M2=kg/(m·s));Q为体积流量,这里用来测量流量而不是根据Q=π/的平均速度 4Dc2<v> (立方米/秒)。
水头损失形式
编辑水头损失Δh(或hf)表示以工作流体柱的等效高度表示的摩擦引起的压力损失,因此压降为
Δ p = ρ g Δ h
Δh = 在给定长度的管道上由于管道摩擦引起的水头损失(SI 单位:m);g = 由于重力引起的局部加速度(m/s2)。
剪应力形式
编辑管道或明渠中的平均壁面剪应力 τ 用 Darcy–Weisbach 摩擦系数表示为
τ = 1 8 f D ρ ⟨ v ⟩ 2 。
壁面剪切应力的 SI 单位为帕斯卡 (Pa)。
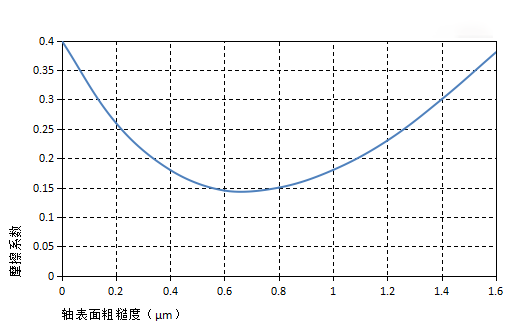
达西摩擦系数
编辑摩擦系数 fD 不是一个常数:它取决于管道的特性(直径 D 和粗糙度 ε)、流体的特性(其运动粘度 ν [nu])和流体的速度 流 ⟨v⟩。 它已在某些流量范围内以高精度测量,可以通过使用各种经验关系进行评估。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/206543/
