帕斯卡定律

固体力学

• 变形
• 弹性
  • 线性
• 可塑性
• 胡克定律
• 压力
• 有限应变
• 无穷小应变
• 兼容性
• 弯曲
• 联系技师
  • 摩擦
• 材料失效理论
• 断裂力学

流体力学流变学

科学家们

• 伯努利
• 波义耳
• 柯西
• 查尔斯
• 欧拉
• 菲克
• 盖-吕萨克
• 格雷厄姆
• 胡克
• 牛顿
• 纳维
• 诺尔
• 帕斯卡
• 斯托克斯
• 特鲁斯戴尔

帕斯卡定律（也称为帕斯卡原理或流体压力传递原理）是布莱斯·帕斯卡提出的流体力学原理，该原理指出受限不可压缩流体中任一点的压力变化会传递到整个流体中，使得 同样的变化无处不在。 该定律由法国数学家布莱斯·帕斯卡于 1653 年创立，并于 1663 年发表。

帕斯卡原理定义为

封闭的静止流体中任一点的压力变化都会原封不动地传递到流体中的所有点。

施加在封闭容器中的流体上的压力均匀且不衰减地传递到容器的所有部分，并与封闭壁成直角作用。

替代定义：施加到封闭液体任何部分的压力将通过液体在各个方向上均等地传递。

该原理在数学上表述为：

Δ p = ρ g ⋅ Δ h {displaystyle Delta p=rho gcdot Delta h,}Δ p {displaystyle Delta p} 是静水压力（在 在 SI 系统中为帕斯卡），或流体柱内两点的压力差，由于流体的重量）；ρ 是流体密度（在 SI 系统中以千克每立方米为单位）；g 是由于加速度 到重力（通常使用由于地球重力引起的海平面加速度，单位为米/秒平方）；Δ h {displaystyle Delta h} 是流体在测量点上方的高度，或与 流体柱内两点之间的高程（以米为单位）。

该公式的直观解释是，两个高度之间的压力变化是由于高度之间的流体重量引起的。 或者，该结果可以解释为由于重力场的存在，单位体积液体的势能变化引起的压力变化。 请注意，随高度的变化不依赖于任何额外的压力。 因此，帕斯卡定律可以解释为在流体的任何给定点施加的任何压力变化都不会减弱地传递到整个流体中。

该公式是 Navier-Stokes 方程的一个特例，没有惯性和粘性项。

如果 U 形管装满水并且在两端放置活塞，则左侧活塞施加的压力将传递到整个液体并作用于右侧活塞的底部（活塞只是可以自由滑动但紧贴内部的塞子 管。）。 左活塞对水施加的压力将完全等于水对右活塞施加的压力 p 1 = p 2 {displaystyle p_{1}=p_{2}} 。 通过使用 p = F A {displaystyle p={frac {F}{A}}} 我们得到 F 1 A 1 = F 2 A 2 ⇔ F 2 F 1 = A 2 A 1 {displaystyle { frac {F_{1}}{A_{1}}}={frac {F_{2}}{A_{2}}}Leftrightarrow {frac {F_{2}}{F_{1 }}}={frac {A_{2}}{A_{1}}}} 。 假设右侧的管子宽 50 倍 A 2 A 1 = 50 {displaystyle {frac {A_{2}}{A_{1}}}=50} 。 如果在左活塞上施加 1 N 的负载 ( F 1 = 1 N {displaystyle F_{1}=1N} )，由于负载的重量，一个额外的压力会传递到整个液体并向上抵靠右活塞 活塞。

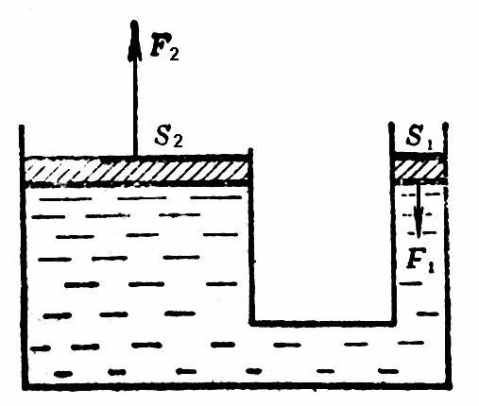
右活塞上的这个额外压力将导致向上的力 F 2 = F 1 A 2 A 1 = 50 N {displaystyle F_{2}=F_{1}{frac {A_{2}}{A_{ 1}}}=50N} 是左活塞上的力的 50 倍。 力和压力之间的差异很重要：附加压力施加在较大活塞的整个区域上。 因为有 50 倍的面积，50 倍的力施加在较大的活塞上。 因此，较大的活塞将支撑 50 N 的载荷——较小活塞上载荷的五十倍。

使用这样的设备可以成倍增加力量。 一牛顿输入产生 50 牛顿输出。 通过进一步增加较大活塞的面积（或减小较小活塞的面积），原则上可以任意倍增力。 帕斯卡原理是液压机操作的基础。