惯性参考系

在经典物理学和狭义相对论中，惯性参考系（也称为惯性参考系、惯性参考系、惯性空间或伽利略参考系）是不经历任何加速度的参考系。 它是一个参考系，其中一个孤立的物理对象——作用在其上的净力为零的物体——被感知为以恒定速度运动（它可能是零速度），或者等效地，它是一个参考系，其中牛顿 的xxx运动定律成立。 所有惯性系都处于一种相对于彼此恒定的直线运动状态； 换句话说，与它们中的任何一个一起移动的加速度计将检测到零加速度。

已经观察到，远离其他物体并且相对于宇宙微波背景辐射处于匀速运动的天体保持这种匀速运动。

一个惯性系中的测量值可以通过简单的变换转换为另一个惯性系中的测量值，即牛顿物理学中的伽利略变换和狭义相对论中的洛伦兹变换。

在分析力学中，惯性参考系可以定义为均匀、各向同性且与时间无关的方式描述时间和空间的参考系。

在广义相对论中

• 在任何小到可以忽略时空曲率和潮汐力的区域中，我们都可以找到一组近似描述该区域的惯性系。
• 一个系统的物理学可以用惯性系来描述，除了由所谓的遥远质量引起的明显影响外，没有相应系统的外部原因。

在非惯性参考系中，从经典物理学和狭义相对论的角度来看，可观测宇宙的基本成分（系统的物理学）之间的相互作用会随着该参考系相对于惯性系的加速度而变化。 从这个角度来看，由于惯性现象，两个物体之间“通常”的物理力必须由明显无源的惯性力来补充。 从广义相对论的角度来看，出现的惯性力（补充的外部原因）归因于时空中的测地线运动。

例如，在经典物理学中，一个落向地面的球不会完全垂直向下移动，因为地球在旋转。 这意味着地球上观察者的参照系不是惯性的。 因此，物理学必须考虑科里奥利效应（一种明显的力）来预测相应的小水平运动。 旋转参考系中出现的视在力的另一个例子涉及离心效应，即离心力。

物体的运动只能相对于其他事物来描述——其他物体、观察者或一组时空坐标。 这些被称为参考系。 如果坐标选择不当，运动定律可能看起来比必要的更复杂。 例如，假设一个没有外力作用的自由体在某一瞬间处于静止状态。 在许多坐标系中，它会在下一瞬间开始移动，即使它没有受力。 但是，始终可以选择一个参考系，使其保持静止。 类似地，如果空间不是统一描述的或时间独立的，则坐标系可以将自由体在空间中的简单飞行描述为其坐标系中的复杂之字形。 事实上，可以给出惯性系的直观总结：在惯性参考系中，力学定律采用最简单的形式。

根据狭义相对论xxx假设，所有物理定律都在惯性系中采取最简单的形式，并且存在多个通过均匀平移相互关联的惯性系：

狭义相对性原理：如果选择一个坐标系 K，使得与其相关的物理定律以最简单的形式适用，则相同的定律适用于任何其他坐标系 K'' 匀速平移 相对于K

—>阿尔伯特·爱因斯坦：广义相对论的基础，A 节，§1

这种简单性体现在惯性系具有独立的物理特性而无需外部原因，而非惯性系中的物理特性具有外部原因。 简单性原理可以用在牛顿物理学和狭义相对论中； 参见 Nagel 和 Blagojević。

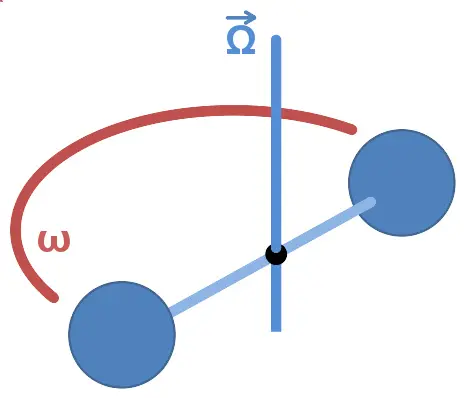
牛顿力学定律并不总是以其最简单的形式成立......例如，如果观察者被放置在一个相对于地球旋转的圆盘上，他/她会感觉到一种“力”将他/她推向 圆盘的xxx。