隐藏吸引子

在分岔理论中，在不失去静止集稳定性的情况下产生的有界振荡称为隐振荡。 在非线性控制理论中，在具有有界状态的时不变控制系统中隐藏振荡的诞生意味着在参数域中跨越边界，其中静止状态的局部稳定性意味着全局稳定性。

如果隐藏振荡（或一组这样的隐藏振荡填充动力系统相空间的紧凑子集）吸引所有附近的振荡，那么它被称为隐藏吸引子。 对于具有全局吸引的唯 一平衡点的动力系统，隐藏吸引子的诞生对应于从单稳态到双稳态的行为质变。

在一般情况下，动力系统可能是多稳态的，并且在相空间中具有共存的局部吸引子。 虽然平凡的吸引子，即稳定的平衡点，可以很容易地通过分析或数值找到，但周期性和混沌吸引子的搜索可能会变成一个具有挑战性的问题。

为了在物理或数值实验中识别局部吸引子，需要在吸引子的吸引力盆地中选择一个初始系统状态，并观察系统状态如何从这个初始状态开始，经过一个瞬态过程后，将吸引子可视化。 吸引子分为隐藏的或自激的，反映了揭示吸引盆和在相空间中寻找局部吸引子的困难。

定义。 如果一个吸引子的吸引盆不与平衡点的某个开放邻域相交，则该吸引子称为隐藏吸引子； 否则称为自激吸引子。

G. Leonov 和 N. Kuznetsov 在 2009 年首次发现隐藏的 Chua 吸引子时引入了隐藏或自激吸引子的分类。 类似地，任意有界振荡，不一定具有开放邻域作为相空间中的吸引盆地，被归类为自激振荡或隐藏振荡。

对于自激吸引子，它的吸引盆与不稳定的平衡有关，因此，可以通过标准计算程序在数值上找到自激吸引子，其中在瞬态过程之后，轨迹从邻域开始 一个不稳定的平衡，被吸引到振荡状态然后追踪它。

因此，自激吸引子，即使在多稳态情况下共存，也可以很容易地在数值上显示和可视化。 在洛伦兹系统中，对于经典参数，吸引子相对于所有存在的平衡是自激的，并且可以通过它们附近的任何轨迹可视化； 然而，对于其他一些参数值，存在两个平凡吸引子与一个混沌吸引子并存的情况，混沌吸引子仅对零平衡是自激吸引子。 Van der Pol、Beluosov–Zhabotinsky、Rössler、Chua、Hénon 动力系统中的经典吸引子是自激的。

一个猜想是自激吸引子的 Lyapunov 维数不超过不稳定平衡之一的 Lyapunov 维数，其不稳定流形与吸引盆相交并可视化吸引子。

隐藏吸引子有吸引盆地，它与平衡点无关，“隐藏”在相空间的某个地方。 例如，隐藏的吸引子是没有平衡的系统中的吸引子：例如，具有 Sommerfeld 效应的旋转机电动力系统（1902 年），在只有一个稳定平衡的系统中：例如，非线性控制系统单稳态的艾泽曼猜想（1949）和卡尔曼猜想（1957）的反例。

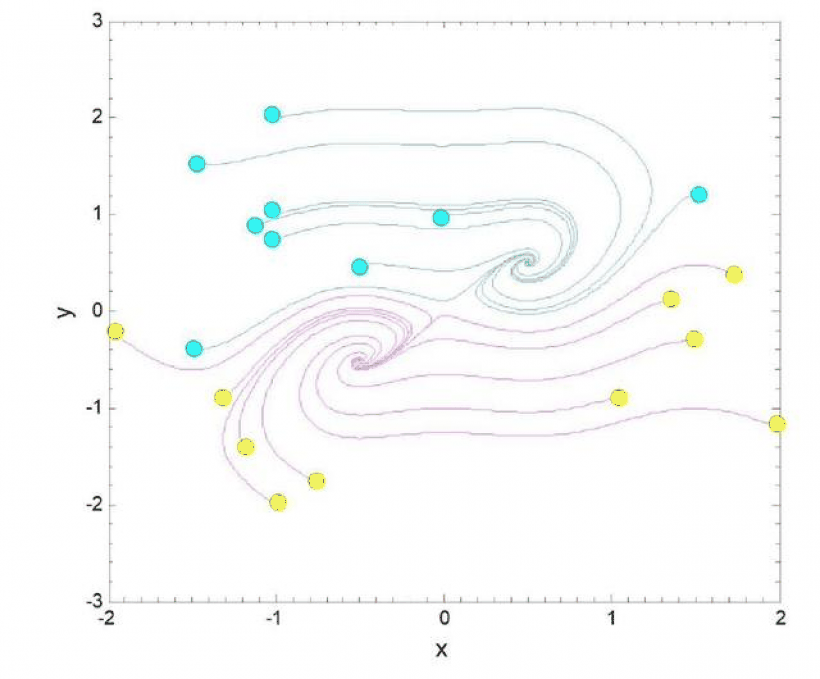
第 一个相关的理论问题是希尔伯特第 16 个问题的第二部分，即二维多项式系统中极限环的数量和相互配置，其中嵌套的稳定极限环是隐藏的周期吸引子。 隐藏吸引子的概念已成为在许多应用动力学模型中发现隐藏吸引子的催化剂。

一般来说，隐藏吸引子的问题是没有通用的直接方法来跟踪或预测系统动态的这种状态。 而对于二维系统，可以使用分析方法研究隐藏的振荡（例如，参见希尔伯特第 16 问题第二部分的结果），用于研究复杂非线性多维中的稳定性和振荡。