布拉格定律

在物理学和化学中，布拉格定律、武尔夫-布拉格条件或劳厄-布拉格干涉，劳厄衍射的一种特殊情况，给出了晶格中波的相干散射角度。 它包括由晶格平面散射的波前的叠加，导致波长和散射角之间存在严格的关系，或者导致相对于晶格的波矢量传输。 这种定律最初是为晶体上的 X 射线制定的。 然而，它适用于各种量子束，包括原子距离的中子和电子波，以及人造周期性微尺度晶格的可见光。

这些晶体在某些特定波长和入射角下会产生强烈的反射辐射峰值。 派生的布拉格定律是劳厄衍射的一种特殊解释，布拉格斯通过从晶格平面反射波以几何方式解释相长的劳厄-布拉格干涉，使得路径差成为入射波长的倍数。

Lawrence Bragg 通过将晶体建模为一组由常数参数 d 分隔的离散平行平面来解释此结果。 有人提出，如果入射 X 射线辐射在各个平面上的反射相长干涉，则会产生布拉格峰。

布拉格衍射的概念同样适用于中子衍射和电子衍射过程。 中子和 X 射线波长都与原子间距离 (~ 150 pm) 相当，因此是该长度尺度的优秀探针。

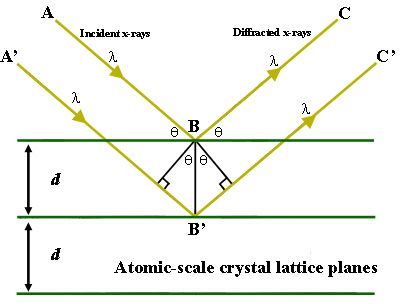
当与原子间距相当的波长 λ 的辐射被晶体系统的原子以镜面方式（镜面反射）散射并经历相长干涉时，就会发生布拉格衍射。 对于结晶固体，波从由连续原子层之间的距离 d 分隔的晶格平面散射。 当散射波建设性地干涉时，它们保持同相。

由于晶格的连续晶面 (h,k,l) 中反射的累积效应（如米勒符号所描述），相长干涉或相消干涉的效果会增强。 这导致布拉格定律，它描述了相长干涉xxx的 θ 条件：

请注意，包括电子、质子和中子在内的运动粒子具有相关的波长，称为德布罗意波长。 通过测量作为散射角函数的散射波强度获得衍射图案。 在散射角满足布拉格条件的点处的衍射图案中获得非常强的强度，称为布拉格峰。 如引言中所述，此条件是更一般的劳厄方程的特例，并且可以证明劳厄方程在附加假设下简化为布拉格条件。

晶格的布拉格衍射现象与薄膜干涉具有相似的特性，在周围介质（如空气）和干涉介质（如油）的折射率相等的极限条件下具有相同的条件。