晶体学限制定理

晶体学限制定理的基本形式是基于观察到晶体的旋转对称性通常限于 2 重、3 重、4 重和 6 重。 然而，准晶体可能会出现其他衍射图案对称性，例如 5 重；

晶体被建模为离散晶格，由一系列独立的有限平移生成。 因为离散性要求格点之间的间距有一个下界，所以格在任何点的旋转对称群必须是一个有限群（或者，该点是xxx允许无限旋转对称的系统）。 该定理的优势在于并非所有有限群都与离散格兼容； 在任何维度上，我们都只有有限数量的兼容组。

2D（墙纸组）和3D（空间组）这两个特例在应用中用的最多，可以放在一起处理。

维度 2 或维度 3 中的旋转对称必须将一个格点移动到同一平面中的一系列其他格点，从而生成共面格点的正多边形。 现在，我们将注意力集中在对称性起作用的平面上。

现在考虑 8 次旋转，以及多边形相邻点之间的位移矢量。 如果任意两个格点之间存在位移，则在格中各处重复相同的位移。 因此，收集所有边缘位移以从单个格点开始。 边缘向量变为径向向量，它们的 8 重对称意味着收集点周围有一个正八边形的格点。 但这是不可能的，因为新的八角形大约是原来的八角形的 80%。 收缩的意义在于它是无限的。 可以用新的八边形重复相同的构造，一次又一次，直到格点之间的距离尽可能小； 因此，没有离散格可以具有 8 重对称性。 同样的论点适用于任何 k 次旋转，k 大于 6。

收缩参数也消除了 5 重对称性。 考虑一个由格点组成的正五边形。 如果它存在，那么我们可以每隔一个边缘位移并（从头到尾）组装一个 5 点星，最后一个边缘返回起点。 这样一颗恒星的顶点也是具有 5 重对称性的正五边形的顶点，但比原来的小了约 60%。

这样定理就得证了。

准晶体的存在表明线性平移的假设是必要的。 可能具有 5 重旋转对称性和离散格，并且 tiling 的任何局部邻域都会重复无限次，但 tiling 整体上没有线性平移。 并且在没有离散格假设的情况下，上述构造不仅没有达到矛盾，反而产生了一个（非离散的）反例。 因此，缺少任何一个假设的论证都不能消除 5 重旋转对称性。 然而，整个（无限）平面的 Penrose 平铺只能具有关于单个点的（整个平铺的）精确 5 重旋转对称，而 4 重和 6 重格子具有无限多个旋转对称中心。

考虑由平移向量 r 分隔的两个格点 A 和 B。 考虑一个角度 α，使得角度 α 围绕任何格子点的旋转是格子的对称性。 围绕点 B 旋转 α 将点 A 映射到新点 A'。 类似地，围绕点 A 旋转 α 可将 B 映射到点 B'。 由于提到的两个旋转都是对称操作，因此 A' 和 B' 必须都是格点。

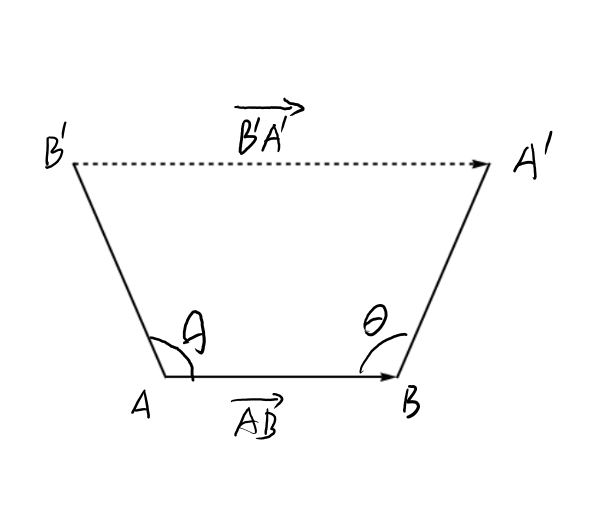
其中 M = m + 1 也是一个整数。 请记住| 余弦⁡α | ≤ 1 我们允许整数 M ∈ { − 2 , − 1 , 0 , 1 , 2 } 。 求解 α 的可能值表明在 0° 到 180° 范围内的xxx值是 0°、60°、90°、120° 和 180°。