晶格能

在化学中，晶格能是一摩尔结晶离子化合物从其组成离子形成时的能量变化，这些离子被假定为最初处于气态。 它是结合离子固体的内聚力的量度。 晶格能的大小与许多其他物理性质有关，包括溶解度、硬度和挥发性。 由于通常无法直接测量，因此晶格能通常通过 Born-Haber 循环从实验数据中推导出来。

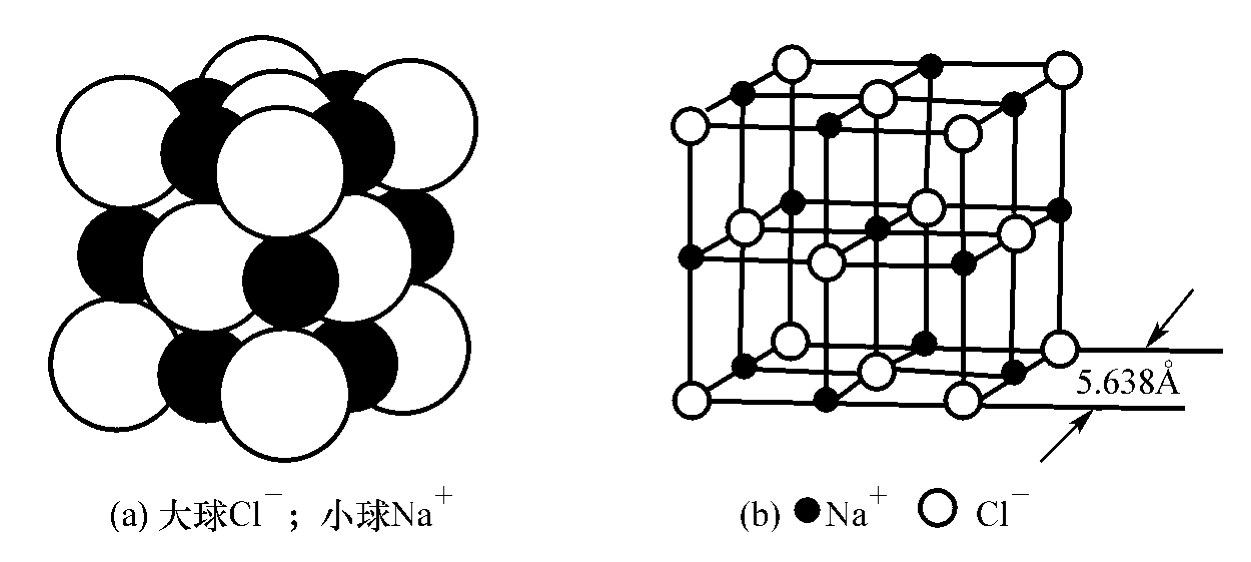
晶格能的概念最初应用于具有岩盐 (NaCl) 和闪锌矿 (ZnS) 等结构的化合物的形成，其中离子占据高对称晶格位置。 对于 NaCl，晶格能是反应的能量变化

Na+ (g) + Cl− (g) → NaCl (s)

相当于-786 kJ/mol。

一些化学教科书以及广泛使用的 CRC 化学和物理手册将晶格能量定义为相反的符号，即在真空中将晶体转化为无限分离的气态离子所需的能量，这是一个吸热过程。 按照这个约定，NaCl 的晶格能量为 +786 kJ/mol。 这两种符号约定都被广泛使用。

压力 P {displaystyle P} 下的晶格能量和晶格焓之间的关系由以下等式给出：

Δ U l a t t i c e = Δ H l a t t i c e − P Δ V m {displaystyle Delta U_{lattice}=Delta H_{lattice}-PDelta V_{m}} ,

其中 Δ U l a t t i c e {displaystyle Delta U_{lattice}} 是晶格能量（即摩尔内能变化）， Δ H l a t t i c e {displaystyle Delta H_{lattice}} 是晶格焓， 和 Δ V m {displaystyle Delta V_{m}} 由于晶格的形成，摩尔体积的变化。 由于固体的摩尔体积远小于气体的摩尔体积，所以ΔVm＜； 0 {displaystyle Delta V_{m}<0} 。 由于所涉及的净吸引力，在真空中由离子形成晶格必须降低内能，因此 Δ U l a t t i c e <; 0 {displaystyle Delta U_{lattice}<0} 。 − P Δ V m {displaystyle -PDelta V_{m}} 项是正的，但在低压下相对较小，因此晶格焓的值也是负的（并且是放热的）。

离子化合物的晶格能量在很大程度上取决于构成固体的离子的电荷，它们必须通过库仑定律相互吸引或排斥。 更微妙的是，离子的相对和xxx大小会影响 Δ H l a t t i c e {displaystyle Delta H_{lattice}} 。 伦敦色散力也存在于离子之间，并通过极化效应贡献晶格能量。 对于由分子阳离子和/或阴离子组成的离子化合物，如果任一分子具有分子偶极矩，则也可能存在离子-偶极和偶极-偶极相互作用。 下面描述的理论处理集中于由原子阳离子和阴离子组成的化合物，而忽略了热化晶格振动对晶格内能的贡献。

1918 年，Born 和 Landé 提出晶格能可以从离子晶格的电势和排斥势能项中推导出来。

NA为阿伏加德罗常数；M为马德隆常数，与晶体的几何结构有关；z+为阳离子的电荷数；z−为阴离子的电荷数；e为基本电荷，等于1.6022×10 −19 C；ε0为自由空间的介电常数，等于8.854×10−12 C2 J−1 m−1；r0为离子间的最近邻距离； n 是玻恩指数（介于 5 和 12 之间的数字，通过测量固体的可压缩性通过实验确定，或从理论上得出）。

上面的 Born–Landé 方程表明化合物的晶格能量主要取决于两个因素：

• 随着离子电荷的增加，晶格能量增加（变得更负），
• 当离子靠得更近时，晶格能量增加（变得更负）

例如，氧化钡 (BaO) 具有 NaCl 结构，因此具有相同的马德隆常数，键半径为 275 皮米，晶格能为 −3054 kJ/mol，而氯化钠 (NaCl) 的键半径为 283 皮米，晶格能量为 −786 kJ/mol。 键半径相似但电荷数不同，BaO 的电荷数为 (+2,-2)，NaCl 的电荷数为 (+1,-1)； Born-Landé 方程预测电荷数的差异是晶格能量差异很大的主要原因。