半衰期

半衰期（符号 t½）是（物质）数量减少到其初始值的一半所需的时间。 该术语在核物理学中常用来描述不稳定原子经历放射性衰变的速度或稳定原子存活的时间。 该术语还更广泛地用于描述任何类型的指数（或很少见的非指数）衰减。 例如，医学指的是药物和其他化学物质在人体内的生物半衰期。 半衰期（呈指数增长）的反面是倍增时间。

半衰期的最初术语可追溯到1907年欧内斯特·卢瑟福发现该原理，在50年代初缩短为半衰期。 卢瑟福利用放射性元素半衰期的原理，通过测量镭对铅 206 的衰变周期来确定岩石的年龄。

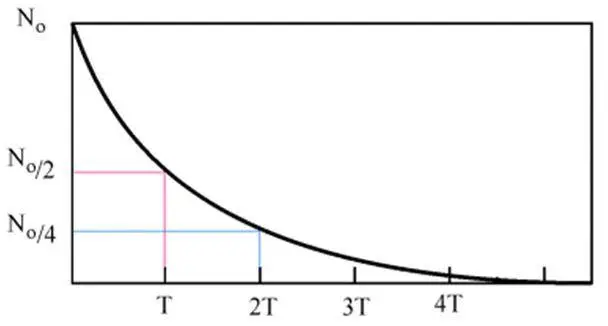
半衰期在指数衰减量的整个生命周期内是常数，它是指数衰减方程的特征单位。 下表显示了数量的减少与经过的半衰期数的关系。

半衰期通常描述离散实体的衰变，例如放射性原子。 在那种情况下，使用声明半衰期是恰好一半实体衰变所需的时间的定义是行不通的。 例如，如果只有一个放射性原子，它的半衰期是一秒钟，那么一秒钟之后就没有半个原子了。

相反，半衰期是根据概率定义的：半衰期是恰好一半的实体平均衰变所需的时间。 换句话说，放射性原子在其半衰期内衰变的概率为 50%。

例如，右图是许多相同原子经历放射性衰变的模拟。 请注意，在一个半衰期之后，由于过程中的随机变化，不会精确地剩下一半的原子，只有大约一半。 然而，当有许多相同的原子衰变时（右方框），大数定律表明，半衰期后半数原子仍然存在是一个非常好的近似。

各种简单的练习可以证明概率衰减，例如涉及抛硬币或运行统计计算机程序。

• N0 是会衰变的物质的初始量（这个量可以用克、摩尔、原子数等来衡量），
• N(t) 是在时间 t 后仍然存在且尚未衰减的量，
• t½ 是衰减量的半衰期，
• τ是一个正数，称为衰减量的平均寿命，
• λ是一个正数，称为衰减量的衰减常数。

在化学动力学中，半衰期的值取决于反应级数：

• 零级动力学：这种反应的速率不依赖于底物浓度，[A]: d [ A ] / d t = − k {\displaystyle d[{\ce {A}}] /dt=-k} 零级动力学的综合速率定律是： [ A ] = [ A ] 0 − k t {\displaystyle [{\ce {A}}]=[{\ce {A}} ]_{0}-kt} 为了找到半衰期，我们必须将浓度值替换为初始浓度除以 2： [ A ] / 2 = [ A ] 0 − k t 1 / 2 {\ displaystyle [{\ce {A}}]/2=[{\ce {A}}]_{0}-kt_{1/2}} 并隔离时间：t 1 / 2 = [ A ] 0 2 k {\displaystyle t_{1/2}={\frac {[{\ce {A}}]_{0}}{2k}}} 这个 t½ 公式表明零的半衰期 有序反应取决于初始浓度和速率常数。

• 一级动力学：在一级反应中，反应物的浓度将呈指数下降 [ A ] = [ A ] 0 e x p ( − k t ) {\displaystyle [{\ce {A}}]=[{ \ce {A}}]_{0}exp(-kt)} 随着时间的推移直到它达到零，半衰期将保持不变，与浓度无关。[A] 的时间 t½ 从 [ 一级反应中的 A]0 到 1/2[A]0