主量子数

在量子力学中，主量子数（符号为 n）是分配给原子中每个电子的四个量子数之一，用于描述该电子的状态。 它的值是自然数（从 1 开始），使其成为离散变量。

除主量子数外，束缚电子的其他量子数是方位角量子数ℓ、磁量子数ml和自旋量子数s。

随着 n 的增加，电子也处于更高的能量，因此与原子核的结合不那么紧密。 平均而言，对于更高的 n，电子离原子核更远。 对于 n 的每个值，都有 n 个可接受的 ℓ（方位角）值，范围从 0 到 n - 1（含），因此更高的 n 电子态更多。 考虑到两种自旋状态，每个 n 壳层最多可容纳 2n2 个电子。

在下面描述的一个简单的单电子模型中，电子的总能量是主量子数 n 的负二次反函数，导致每个 n > 1 的退化能级。 1. 在更复杂的系统中——那些具有核-电子库仑力以外的力的系统——这些能级分裂。 对于多电子原子，这种分裂会产生由 ℓ 参数化的子壳层。 仅基于 n 的能级描述对于从 5（硼）开始的原子序数逐渐变得不足，并且对于钾（Z = 19）及之后的原子序数完全失败。

最初创建主量子数是为了在原子的半经典玻尔模型中使用，以区分不同的能级。 随着现代量子力学的发展，简单的玻尔模型被更复杂的原子轨道理论所取代。 然而，现代理论仍然需要主量子数。

有一组与原子能态相关的量子数。 四个量子数 n、ℓ、m 和 s 指定原子中单个电子的完整且xxx的量子态，称为其波函数或轨道。 由于泡利不相容原理，属于同一原子的两个电子不能对所有四个量子数具有相同的值。 薛定谔波动方程简化为三个方程，求解后可得出前三个量子数。 因此，前三个量子数的方程都是相互关联的。 主量子数出现在波动方程的径向部分的解中，如下所示。

薛定谔波动方程用相应的实数 En 和确定的总能量，即 En 的值来描述能量本征态。 氢原子中电子的束缚态能量由下式给出： E n = E 1 n 2 = − 13.6 eV n 2 , n = 1 , 2 , 3 , … {displaystyle E_{n}={ frac {E_{1}}{n{2}}}={frac {-13.6{text{ eV}}}{n{2}}},quad n=1,2,3, ldots }

参数 n 只能取正整数值。 能级和符号的概念取自早期的玻尔原子模型。 薛定谔方程将这一想法从平面二维玻尔原子发展为三维波函数模型。

在玻尔模型中，允许的轨道是根据方程 L = n ⋅ ℏ = n ⋅ h 2 π {displaystyle L=ncdot hbar =ncdot {h 超过 2pi }}

其中 n = 1, 2, 3, ... 称为主量子数，h 是普朗克常数。 这个公式在量子力学中是不正确的，因为角动量大小是由方位角量子数描述的，但能级是准确的，并且经典地它们对应于电子的势能和动能之和。

主量子数 n 表示每个轨道的相对总能量。 每个轨道的能级随着它与原子核距离的增加而增加。 具有相同 n 值的轨道组通常称为电子壳层。

在任何波-物质相互作用过程中交换的最小能量是波频率乘以普朗克常数的乘积。 这导致波显示出称为量子的粒子状能量包。 具有不同n的能级之间的差异决定了元素的发射光谱。

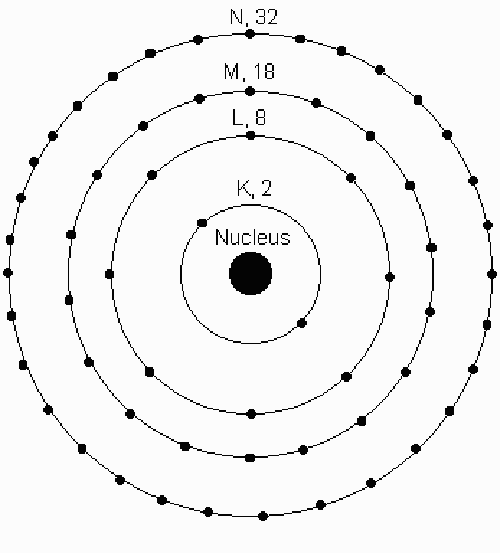
在元素周期表的符号中，电子的主要壳被标记为：

K（n = 1），L（n = 2），M（n = 3）等。

基于主量子数。

主量子数与径向量子数 nr 的关系为：

n = n r + ℓ + 1 {displaystyle n=n_{r}+ell +1}

其中 ℓ 是方位角量子数，nr 等于径向波函数中的节点数。

粒子在公共库仑场和离散谱中运动的确定总能量由下式给出： E n = − Z 2 ℏ 2 2 m 0 a B 2 n 2 = − Z 2 e 4 m 0 2 ℏ 2 n 2 , {displaystyle E_{n}=-{frac {Z{2}hbar {2}}{2m_{0}a_{B}{2}n{2}}}=-{ frac {Z{2}e{4}m_{0}