正则变换
编辑在哈密顿力学中,正则变换是正则坐标 (q, p, t) → (Q, P, t) 的变化,它保留了哈密顿方程的形式。 这有时被称为形式不变性。 它不需要保留哈密顿量本身的形式。 正则变换本身就很有用,而且还构成了哈密顿-雅可比方程(一种计算守恒量的有用方法)和刘维尔定理(本身就是经典统计力学的基础)的基础。
由于拉格朗日力学基于广义坐标,坐标 q → Q 的变换不会影响拉格朗日方程的形式,因此,如果我们同时将动量改变 a,则不会影响哈密尔顿方程的形式 勒让德变换为 P i = ∂ L ∂ Q ˙ i 。 {dISPlaystyle P_{i}={frac {partial L}{partial {dot {Q}}_{i}}}.}
因此,坐标变换(也称为点变换)是一种规范变换。 然而,规范变换的类别要广泛得多,因为旧的广义坐标、动量甚至时间都可以组合起来形成新的广义坐标和动量。 不明确包含时间的正则变换称为受限规范变换(许多教科书只考虑这种类型)。
为清楚起见,我们将此处的介绍限制在微积分和经典力学。 熟悉更高级数学(例如余切束、外导数和辛流形)的读者应该阅读相关的辛同胚文章。 (正则变换是辛同构的特例。)然而,本文末尾包含对现代数学描述的简要介绍。
符号
编辑黑体字变量,如 q 表示不需要像旋转矢量那样变换的 N 个广义坐标的列表
变量或列表上的点表示时间导数
相同坐标数的两个列表之间的点积表示法是对应分量乘积之和的简写
点积(也称为内积)将两个坐标列表映射到一个表示单个数值的变量中。
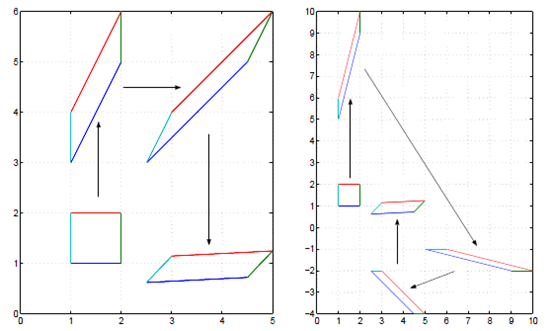
间接方法
编辑一般来说,变换 (q, p, t) → (Q, P, t) 不会保留哈密顿方程的形式。 对于 (q, p) 和 (Q, P) 之间的时间独立变换,我们可以检查变换是否是受限规范的,如下所示。 由于受限变换没有明确的时间依赖性(根据定义)
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/216850/
