相位
编辑在物理和数学中,某个实变量 t的周期函数 F 的相位是一个类似角度的量,表示覆盖到 t 的周期分数。 它被表示为 ϕ ( t ) 并以这样的比例表示,当变量 t 经历每个周期时它会变化一整圈。 它可以用任何角度单位测量,例如度数或弧度,因此随着变量 t 完成一个完整周期,增加 360° 或 2 π。
这种约定特别适用于正弦函数,因为它在任何参数 t 的值都可以表示为 ϕ ( t ) ,相位的正弦, 乘以一些因素(正弦波的幅度)。 (余弦可以用来代替正弦,这取决于人们认为每个周期从哪里开始。)
通常,在表示相位时忽略整圈; 因此 ϕ ( t ) 也是一个周期函数,与 F 具有相同的周期,重复扫描与 t 经历每个时期。
相位 ϕ ( t ) 的数值取决于每个周期起点的任意选择,以及每个周期要映射到的角度区间。
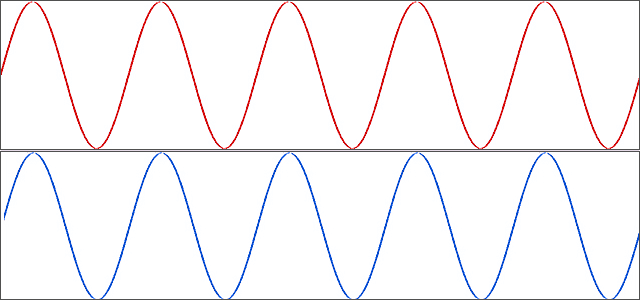
当比较周期函数 F 和它的移位版本 G 时,也使用术语相位。 如果 t 的偏移表示为周期的一小部分,然后缩放到跨越一整圈的角度 φ,则可以得到相移、相位偏移或 G 相对于 F 的相位差。 如果 F 是一类信号的规范函数,如 sin ( t ) 是所有正弦信号,则 φ 称为 G 的初始阶段。
数学定义
编辑这个概念可以想象为一个时钟,它的指针以恒定速度转动,每 T 秒转一圈,并在时间 t 0 . 相位 ϕ ( t ) 是从 12:00 位置到手的当前位置的角度,在时间 t ,顺时针测量。
当根据 F 的特征选择原点 t 0 时,相位概念最有用。 例如,对于,一个方便的选择是函数值从零变为正的任何 t。
以度表示的相位(从 0° 到 360°,或从 −180° 到 +180°)的定义方式相同,只是用 360° 代替 2π。
后果
编辑根据上述任何定义,周期信号的相位 ϕ ( t ) 也是周期性的,具有相同的周期 T。
每个周期开始时的相位为零。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/216944/
