应力-应变曲线

在工程和材料科学中，材料的应力-应变曲线给出了应力和应变之间的关系。 它是通过逐渐向试样施加载荷并测量变形而获得的，由此可以确定应力和应变。 这些曲线揭示了材料的许多特性，例如杨氏模量、屈服强度和极限抗拉强度。

一般来说，表示任何变形形式下应力与应变关系的曲线都可以看作是应力-应变曲线。 应力和应变可以是法向的、剪切的或混合的，也可以是单轴的、双轴的或多轴的，甚至随时间变化。 变形的形式可以是压缩、拉伸、扭转、旋转等。 如无特别说明，应力-应变曲线是指在拉伸试验中测得的材料轴向正应力与轴向正应变之间的关系。

考虑一根原始横截面积为 A 0 的杆，其两端受到相等且相反的力 F 拉动，因此杆处于张力之下。 材料承受的应力定义为力与杆的横截面积之比，以及轴向伸长率：

σ = F A 0 = L − L 0 L 0 = Δ L L 0

下标 0 表示样本的原始维度。 压力的 SI 单位是牛顿每平方米，或帕斯卡（1 帕斯卡 = 1 Pa = 1 N/m2），而应变是无单位的。 这种材料的应力-应变曲线是通过拉长样品并记录应力随应变变化直到样品断裂而绘制的。 按照惯例，应变设置为水平轴，应力设置为垂直轴。 请注意，出于工程目的，我们通常假设材料的横截面积在整个变形过程中不会发生变化。 这是不正确的，因为实际面积会随着弹性和塑性变形而变形而减少。 以原始截面和标距长度为基础的曲线称为工程应力-应变曲线，以瞬时截面积和长度为基础的曲线称为真实应力-应变曲线。 除非另有说明，否则通常使用工程应力-应变。

由于截面积缩小，忽略了伸长率对进一步伸长率的影响，真实应力应变不同于工程应力应变。

σ t = F A

这里的维度是瞬时值。 假设样品的体积守恒并且变形均匀发生，

A 0 L 0 = A L

真实的应力和应变可以用工程应力和应变来表示。 对于真正的压力，

σ t = F A = F A 0 A 0 A = F A 0 L L 0 = σ ( 1 + ε )

整合双方并应用边界条件，

ε t = ln ⁡ ( L L 0 ) = ln ⁡ ( 1 + ε )

所以在拉伸试验中，真应力大于工程应力，真应变小于工程应变。 因此，定义真实应力-应变曲线的点向上和向左移动以定义等效的工程应力-应变曲线。 真实和工程应力和应变之间的差异将随着塑性变形而增加。 在低应变下，两者之间的差异可以忽略不计。

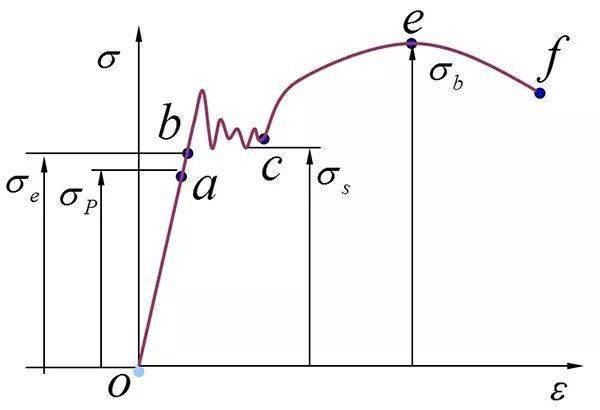
对于抗拉强度点，它是工程应力-应变曲线中的极大点，而不是真实应力-应变曲线中的特殊点。 因为工程应力与沿样品施加的力成正比，颈缩形成的标准可以设置为 δ F = 0  。

δ F = σ t δ A + A δ σ t = 0

该分析表明了 UTS 点的性质。 功加固效果恰好与UTS点截面积的缩小相平衡。