吸引子

在动力系统的数学领域中，吸引子是系统趋于进化的一组状态，用于系统的各种起始条件。 足够接近吸引子值的系统值即使受到轻微干扰也能保持接近。

在有限维系统中，演化变量可以用代数表示为 n 维向量。 吸引子是n维空间中的一个区域。 在物理系统中，n维可以是例如一个或多个物理实体中的每一个的两个或三个位置坐标； 在经济系统中，它们可能是单独的变量，例如通货膨胀率和失业率。

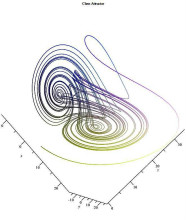
如果演化变量是二维或三维的，则动态过程的吸引子可以在二维或三维中以几何方式表示（例如在右侧描述的三维情况下）。 吸引子可以是一个点、一组有限的点、一条曲线、一个流形，甚至是一个具有分形结构的复杂集合，称为奇异吸引子（请参阅下面的奇异吸引子）。 如果变量是标量，则吸引子是实数线的子集。 描述混沌动力系统的吸引子一直是混沌理论的成就之一。

吸引子中动力系统的轨迹不必满足任何特殊约束，除了保持在吸引子上，及时向前。 轨迹可能是周期性的或混乱的。 如果一组点是周期性的或混沌的，但邻域中的流远离该集合，则该集合不是吸引子，而是称为排斥器（或排斥器）。

动力系统通常由一个或多个微分或差分方程描述。 给定动力系统的方程指定了它在任何给定的短时间内的行为。 为了确定系统在较长时期内的行为，通常需要通过分析方法或迭代对方程进行积分，通常需要借助计算机。

物理世界中的动力系统往往源于耗散系统：如果没有某种驱动力，运动就会停止。 （耗散可能来自内部摩擦、热力学损失或材料损失等多种原因。）耗散和驱动力趋于平衡，消除初始瞬变并使系统稳定到其典型行为。 典型行为对应的动力系统相空间的子集是吸引子，也称为吸引部分或被吸引子。

不变集和极限集类似于吸引子的概念。 不变集是在动力学下向自身演化的集合。 吸引子可能包含不变集。 极限集是一组点，因此存在一些初始状态，随着时间趋于无穷大，该初始状态最终任意接近极限集（即集合中的每个点）。 吸引子是极限集，但并非所有极限集都是吸引子：系统的某些点可能会收敛到极限集，但不同的点在稍微偏离极限集时可能会被撞掉，永远不会回到极限集 极限集附近。

例如，阻尼摆有两个不变点：最小高度点 x0 和xxx高度点 x1。 点 x0 也是一个极限集，因为轨迹会收敛到它； 点 x1 不是极限集。 由于空气阻力引起的耗散，x0 点也是吸引子。 如果没有耗散，x0 就不是吸引子。 亚里士多德认为，物体只有在受到推动时才会移动，这是耗散吸引子的早期表述。

已知一些吸引子是混沌的（参见奇异吸引子），在这种情况下，吸引子的任何两个不同点的演化都会导致轨迹呈指数发散，即使系统中存在最小的噪声，这也会使预测复杂化。

设 t 表示时间，f(t, •) 是指定系统动力学的函数。 也就是说，如果 a 是 n 维相空间中的一个点，表示系统的初始状态，则 f(0, a) = a 并且对于正值 t，f(t, a) 是 t 单位时间后该状态演化的结果。 例如，如果系统描述一维自由粒子的演化，则相空间是坐标为 (x,v) 的平面 R2，其中 x 是粒子的位置，v 是它的速度，a = (x ,v), 演化由下式给出

f ( t , ( x , v ) ) = ( x + t v , v ) 。

吸引子是相空间的子集 A，具有以下三个条件：

• A 在 f 下是前向不变的：如果 a 是 A 的元素，那么 f(t,a) 也是，对于所有 t >; 0.
• 存在 A 的邻域，称为 A 的吸引力盆地