基尔霍夫衍射公式
编辑基尔霍夫衍射公式可用于对光在各种配置中的传播进行建模,无论是通过分析还是使用数值建模。 当单色球面波是所考虑情况的入射波时,它给出了波扰动的表达式。 该公式是通过将基尔霍夫积分定理应用于具有某些近似值的球面波而导出的,该定理使用格林的第二恒等式推导出齐次标量的解。
惠更斯-菲涅耳原理是由菲涅耳-基尔霍夫衍射公式推导出来的。
基尔霍夫连射公式的推导
编辑基尔霍夫积分定理,有时也称为菲涅耳-基尔霍夫积分定理,利用格林的第二恒等式,根据波动方程的解推导出齐次标量波动方程在任意空间位置P的解 及其在任意封闭曲面 S {dISPlaystyle S} 上所有点的一阶导数作为包含 P 的某个体积的边界。
积分定理为单色源提供的解是 U ( P ) = 1 4 π ∫ S [ U ∂ ∂ n ( e i k s s ) − e i k s s ∂ U ∂ n ] d S ,其中 U 是齐次标量波动方程解的空间部分(即 V ( r , t ) = U ( r ) e − i ω t 作为 齐次标量波动方程解),k 是波数,s 是从 P 到(无限小)积分表面元素的距离,并且 ∂ ∂ n 表示沿积分表面元素法线单位向量 n的微分(即法线导数),即 ∂ f ∂ n = ∇ f ⋅ n 。 请注意,在这个积分中,表面法线或 n的方向朝向封闭体积的内部; 如果使用更常见的指向外的法线,则积分将具有相反的符号。 还要注意,在此处显示的积分定理中,n 和 P 是矢量,而其他项是标量。
对于以下情况,做出以下基本假设。
- 点波源到积分区的距离、积分区到观察点P的距离、开口尺寸S都远大于波的波长λ .
- U 和 ∂ U ∂ n = ∇ U ⋅ n 在孔径的边界处是不连续的,称为基尔霍夫边界条件。 这可能与另一个假设有关,即孔径(或开放区域)上的波浪与在没有波浪障碍物的情况下会出现的波浪相同。
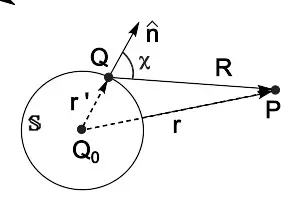
点源
编辑考虑 P0 处的单色点光源,它照亮屏幕上的孔径。 点源发射的波的强度随着行进距离的平方反比而衰减,因此振幅随着距离的倒数而衰减。 距离 r {diSPlaystyle r} 处扰动的复振幅由下式给出
U ( r ) = a e i k r r ,其中 a 表示点源处扰动的大小 .
通过将基尔霍夫积分定理应用于半径为 R 的球体与屏幕相交形成的封闭曲面,可以找到空间位置 P 处的扰动。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/217774/
