德拜模型

在热力学和固态物理学中，德拜模型是彼得德拜于 1912 年开发的一种方法，用于估计固体中声子对比热（热容量）的贡献。 它将原子晶格的振动（热）视为盒子中的声子，这与爱因斯坦光电子模型形成对比，爱因斯坦光电子模型将固体视为许多独立的、非相互作用的量子谐振子。 德拜模型正确地预测了固体热容量的低温依赖性，它与 T 3 {displaystyle T{3}} – 德拜 T 3 定律成正比。 就像爱因斯坦光电子模型一样，它也恢复了高温下的独龙-珀蒂定律。 但由于简化假设，它的准确性在中间温度下受到影响。

德拜模型是普朗克黑体光子辐射定律的固态等价物，其中将电磁光子辐射视为光子气体。 德拜模型将原子振动视为盒子中的声子（盒子是固体）。 大多数计算步骤是相同的，因为两者都是具有线性色散关系的无质量 Bose 气体的示例。

考虑边长为 L {displaystyle L} 的立方体。 从盒子文章中的粒子，盒子内声波扰动的共振模式（现在只考虑与一个轴对齐的那些）的波长由下式给出

λ n = 2 L n , {displaystyle lambda _{n}={2L over n},,}

其中 n {displaystyle n} 是一个整数。 声子的能量是

E n = h ν n , {displaystyle E_{n} =hnu _{n},,}

其中 h {displaystyle h} 是普朗克常数，而 ν n {displaystyle nu _{n}} 是声子的频率。 近似地认为频率与波长成反比，我们有

E n = h ν n = h c s λ n = h c s n 2 L , {displaystyle E_{n}=hnu _{n}={hc_{rm {s}} over lambda _ {n}}={hc_{s}n 超过 2L},,}

其中 c s {displaystyle c_{s}} 是固体内的声速。

频率与波长成反比（给出恒定的声速）的近似值适用于低能声子，但不适用于高能声子（请参阅有关声子的文章）。 这种分歧是德拜模型的局限之一。 它在中间温度下产生不正确的结果，而在低温和高温极限下结果是准确的。

其中 N ¯ ( E n ) {displaystyle {bar {N}}(E_{n})} 是能量为 E n {displaystyle E_{n}} 的盒子中声子的数量。 换句话说，总能量等于能量乘以具有该能量的声子数量（一维）的总和。 在 3 个维度中，在这里，德拜模型和普朗克黑体光子辐射定律不同。 与盒子中的电磁光子辐射不同，声子能态的数量是有限的，因为声子不能具有任意高的频率。 它的频率受其传播介质——固体的原子晶格的限制。 考虑下面的横向声子的图示。

假设声子的最小波长是原子间距的两倍是合理的，如下图所示。 固体中有 N {displaystyle N} 原子。 我们的实体是一个立方体，这意味着每条边有 N 3 {displaystyle {sqrt[{3}]{N}}} 个原子。 原子间隔由 L / N 3 {displaystyle L/{sqrt[{3}]{N}}} 给出，最小波长为

λ m i n = 2 L N 3 , {displaystyle lambda _{rm {min}}={2L over {sqrt[{3}]{N}}},,}

使xxx模式数 n {displaystyle n} （光子无限）

n m a x = N 3 。 {displaystyle n_{rm {max}}={sqrt[{3}]{N}},.}

这个数字限制了三重能量总和的上限

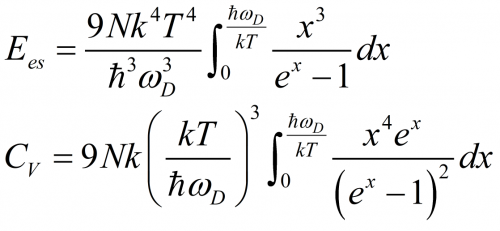
对于变化缓慢、性能良好的函数，可以用积分代替求和（也称为 Thomas–Fermi 近似）

到目前为止，还没有提到 N ¯ ( E ) {displaystyle {bar {N}}(E)}