细胞自动机

元胞自动机（pl.cellular automata，缩写CA）是自动机理论中研究的一种离散计算模型。 元胞自动机也称为元胞空间、镶嵌自动机、均质结构、元胞结构、镶嵌结构和迭代阵列。 元胞自动机已在各个领域得到应用，包括物理学、理论生物学和微观结构建模。

元胞自动机由规则的细胞网格组成，每个细胞处于有限数量的状态之一，例如开和关（与耦合映射格相反）。 网格可以是任意有限维数。 对于每个像元，一组称为其邻域的像元是相对于指定像元定义的。 通过为每个单元格分配一个状态来选择初始状态（时间 t = 0）。 根据一些固定规则（通常是数学函数）创建新的一代（将 t 推进 1），该规则根据单元格的当前状态及其邻域单元格的状态确定每个单元格的新状态 . 通常，更新单元格状态的规则对于每个单元格都是相同的，并且不会随时间改变，并且会同时应用于整个网格，但也有例外，例如随机元胞自动机和异步元胞自动机。

这个概念最初是在 1940 年代由 Stanislaw Ulam 和 John von Neumann 在洛斯阿拉莫斯国家实验室同时发现的。 虽然在整个 1950 年代和 60 年代都有一些人进行研究，但直到 1970 年代和康威的二维元胞自动机“生命游戏”，人们对该主题的兴趣才扩展到学术界之外。 20 世纪 80 年代，Stephen Wolfram 从事一维元胞自动机的系统研究，他称之为初等元胞自动机； 他的研究助理 Matthew Cook 证明其中一条规则是图灵完备的。

正如 Wolfram 概述的那样，元胞自动机的主要分类编号为 1 到 4。 按顺序，它们是模式通常稳定为同质性的自动机，模式演化为基本稳定或振荡结构的自动机，模式以看似混乱的方式演化的自动机，以及模式变得极其复杂并可能持续一段时间的自动机 很长一段时间，具有稳定的局部结构。 最后一类被认为是计算通用的，或者能够模拟图灵机。 特殊类型的元胞自动机是可逆的，其中只有一个配置直接导致后续配置，并且是极权的，其中单个单元的未来值仅取决于一组相邻单元的总值。 元胞自动机可以模拟各种真实世界的系统，包括生物和化学系统。

模拟二维元胞自动机的一种方法是使用一张无限长的方格纸以及一组元胞遵循的规则。 每个正方形称为一个单元格，每个单元格有两种可能的状态，黑色和白色。 单元格的邻域是附近的单元格，通常是相邻的单元格。 两种最常见的邻域类型是冯诺依曼邻域和摩尔邻域。 前者以创始人元胞自动机理论家的名字命名，由四个正交相邻的单元组成。 后者包括 von Neumann 邻域以及四个对角线相邻的单元格。 对于这样的单元及其摩尔邻域，有 512 (= 29) 种可能的模式。 对于 512 种可能模式中的每一种，规则表都会说明中心单元格在下一个时间间隔内是黑色还是白色。 康威的生命游戏是该模型的流行版本。 另一种常见的邻域类型是扩展的冯诺依曼邻域，它包括每个正交方向上最近的两个单元，总共八个。 这种规则系统的一般方程是 kks，其中 k 是单元格可能状态的数量，s 是用于确定单元格的下一个单元格的相邻单元格（包括要计算的单元格本身）的数量 状态。 因此，在具有摩尔邻域的二维系统中，可能的自动机总数为 229，即 1.34×10154。

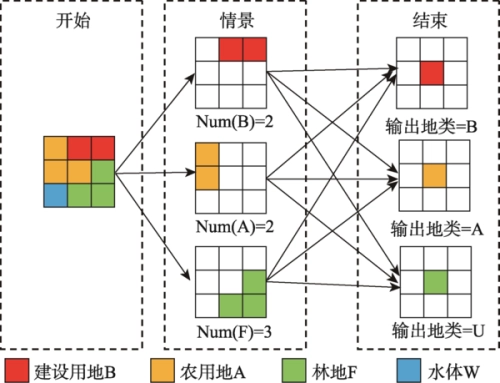
通常假设宇宙中的每个细胞都以相同的状态开始，除了有限数量的处于其他状态的细胞； 状态值的分配称为配置。 更一般地说，有时假设宇宙开始时覆盖有周期性模式，并且只有有限数量的细胞违反了该模式。 后一种假设在一维元胞自动机中很常见。

元胞自动机通常在有限网格而不是无限网格上模拟。 在二维空间中，宇宙将是一个矩形而不是一个无限大的平面。 有限网格的明显问题是如何处理边缘上的单元格。