平均数
编辑平均数(也就是简称,也就是平均数)是给定的数按照一定的计算规则求出的数。 算术、几何和二次平均的计算规则是通用的。 平均数或平均数通常表示算术平均数。
在统计学中,平均数是表征分布典型值或表示分布集中趋势的参数之一(位置参数)。
算术平均数与分布的期望值密切相关。 平均数是根据现有的具体数值确定的,而期望值是基于理论上的期望频率。
算术平均值的可视化
编辑最常用的平均数,即算术平均数,可以在例如想象在跷跷板上使用同样重的球,由于杠杆定律,它们由三角形(枢轴)平衡。 假设可以忽略梁的重量,则产生平衡的三角形的位置等于球体位置的算术平均值。
三个经典平均数e的定义
编辑下面,x 1 , … , x n 被赋予实数,在统计中例如要计算其平均数的测量值。
算术平均数
算术平均值是给定值的总和除以值的个数。
几何平均值
对于不是根据它们的总和而是根据它们的积来解释的数字,可以计算几何平均值。 为此,将数字相乘并取 n {dISPlaystyle n} 次根,其中 n {diSPlaystyle n} 对应于要平均的数字数。
Harmonic 平均数
当根据单位定义数字时,使用调和平均数。 为此,值的数量除以数字的倒数之和。
使用不同平均数的例子
编辑下面以右边给出的数值表中的七个条目为例,说明平均数的哪个定义有意义。
例如,算术平均值用于计算平均速度,因此这些值被解释为速度:如果一只乌龟首先以每小时 3 米的速度跑了一个小时,然后以每小时 2 米的速度跑了三个小时,然后再次加速到三、四、一小时,每小时五米,7小时21米距离的算术平均值为:
也可以使用调和平均数如果测量不是在相同时间而是在相同距离上进行,则计算平均速度可能很有用。 在这种情况下,表中的值表示覆盖均匀距离的时间:乌龟以每小时 3 米的速度跑完第一米,以每小时 2 米的速度跑完另外 3 米,最后 3 米再次加速米分别为 3、4 和 5 m/h。 7 米距离的平均速度是 157 60 {displaystyle {tfrac {157}{60}}} 小时:
x¯ h a r m = 7 ∑ i = 1 7 1 x i = 7 m ( 1 3 + 1 2 + 1 2 + 1 2 + 1 3 + 1 4 + 1 5 ) h = 7 m 157 60 h ≈ 2 .68 m h
关系
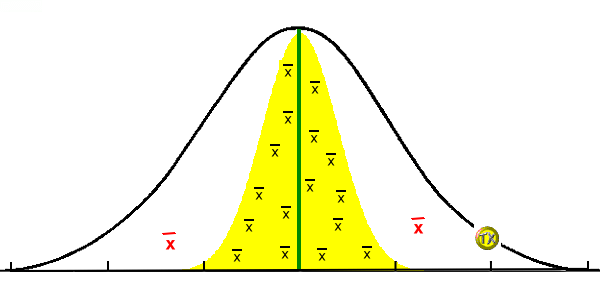
编辑与期望值的关系
平均数和期望值之间的一般区别是平均数应用于特定数据集,而期望值提供有关随机变量分布的信息。 重要的是这两个参数之间的联系。 如果应用均值的数据集是变量分布的样本,则算术平均值是变量均值的无偏且一致的估计量。 由于期望值对应于分布的一阶矩,因此平均数通常用于限制经验数据的分布。 对于完全由前两个矩定义的常用正态分布,平均数因此至关重要。
算术平均值、调和平均值和几何平均值之间的关系
调和平均值的倒数等于数字倒数的算术平均值。
对于 n = 2 {displaystyle n=2} ,平均数 e 以下列方式相互关联:
x h a r m = x g e o m 2 x a r i t h m {displaystyle x_或按几何平均数求解
x geom = x arithm ⋅ x harm 。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/331670/
