曲面

曲面（camber）可以看作空间满足一定条件的点的几何轨迹。如果曲面与方程F(x,y,z)=0满足：①曲面上每一点坐标都满足方程F(x,y,z)=0；②以满足方程F(x,y,z)=0的解为坐标的点都在曲面上，则称F(x,y,z)=0为曲面的方程，而称曲面为此方程的图形。曲面还可以使用参数方程进行表示。

曲面的历史可以追溯到古代文明时期，阿波罗尼亚在总结前人的成就的基础上，再加上自己的研究成果撰写了《圆锥曲线论》8大卷，对于圆锥曲线的研究取得了一定得成就和造诣。古希腊数学家阿基米德（Archimedes）用穷竭法结合力学原理得出并证明了各种复杂的平面曲线围成的面积和各种曲面的面积及其所围成的体积，如抛物线弓形的面积、螺旋线下的面积，球和椭球的表面积与体积，以及圆锥曲线（椭圆，抛物线，双曲线）的旋转体的截体表面积与体积等计算公式。其在曲线的研究中取得了重要进展，他对抛物线和螺旋线的研究为曲面的理论打下了基础。

到18世纪中叶，微分法和积分法得到充分发展，从那时起已经开始了对曲线和曲面理论的本质问题的研究。虽然空间中的曲线和曲面的许多问题与平面曲线相似，但深入研究后，它们逐渐超越了分析学在几何的简单应用，形成了独立的曲线和曲面理论。18世纪后半叶，欧拉（Euler），蒙日（Monge）等数学家参与相关研究，其中欧拉被认为是曲面理论的创立者，并引入平面曲线的内在坐标和曲率概念。欧拉还深入研究了测地线，1736年证明了在无外力作用下，质点在曲面上的匀速运动必然沿测地线进行。这些工作对曲线和曲面理论的发展产生了深远影响。

欧拉

1827年，高斯（Gauss）发表的《关于曲面的一般研究》奠定了曲面微分几何的基础，他发展了曲面理论的普遍方法和问题，并致力于全新的探讨与研究。他建立了由xxx基本形式决定的曲面内在几何，并强调了用参数形式描述曲面的重要性。此外，高斯首次认识到曲面面积与球面对应区域面积之比的极限重要性，并用它表示曲面在一点的曲率。这些贡献对微分几何的发展有深远影响。

高斯

对于微分几何的进一步发展，伟大的数学家波恩哈德·黎曼（Georg Friedrich Bernhard Riemann）作了开创性的工作。黎曼在1851年的博士论文及阿贝尔函数的研究中指出，研究函数不可避免地需要依赖于位置分析学的一些定理。按照现代拓扑学的观点，黎曼实际上已经对闭曲面按亏格分类。值得一提的是，他在学位论文中提出的关于某些函数的全体构成连通闭区域（空间点）的思想，是泛函思想的早期体现。实际上，在黎曼博士论文发表之前，组合拓扑学已有一些零散的研究成果，如欧拉关于闭凸多面体顶点、棱、面数之间关系的著名定理、哥尼斯堡七桥问题和四色问题，这些问题激发了对组合拓扑学（当时称为位置几何学或位置分析学）的深入研究。然而，拓扑学研究的xxx推动力来自于黎曼在复变函数论领域的工作。黎曼在1854年的演讲中，将曲面视为独立的几何实体，而非仅作为欧氏空间中的实体。他认识到曲面上的二次微分形式（即黎曼测度）是外加的结构，而非固定属性。这一发现开创了黎曼几何，为微分几何的进一步发展奠定了基础。后续数学家如李西等人进一步丰富了经典黎曼几何的内容。

波恩哈德·黎曼

如果曲面

与方程

满足：①曲面

上每一点坐标都满足方程

；②以满足方程

的解为坐标的点都在曲面

上，则称

为曲面

的方程，而称曲面

为此方程的图形。曲面

可以看作空间满足一定条件的点的几何轨迹。

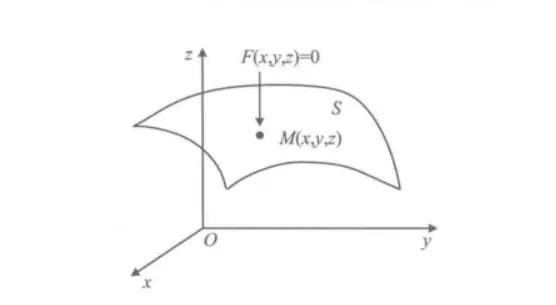
示意图

曲面在建筑学有着广泛的应用，例如，三周期极小曲面（triply periodic minimal surfaces，TPMS）是一类特殊的曲面，也是存在于自然界中的一类结构，其可用于桁架结构的设计，利用三维静力平衡，通过控制标准立方体的细分方式（六面体或四面体细分），构建受力图与结构图的对偶关系。通过将受力图中的封闭单元和内部面分别对应于结构图的节点和边，从而得到如图所示杆状结构近似表达的 TPMS 结构。该方法同样适用于变形的六面体单元。

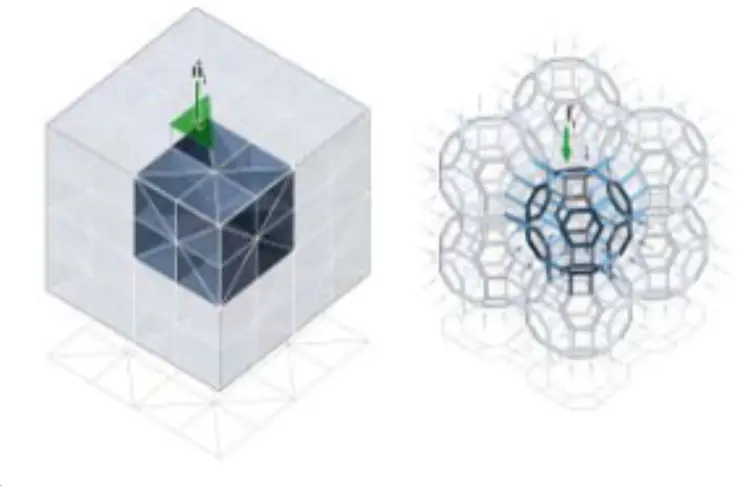
稀疏细分得到杆结构单元

曲面在机械学中有着广泛的作用，例如，主动式曲面打磨技术，只需要3~4遍即可完成岔区钢轨的廓形打磨，通过磨石砂轮和纸砂轮的配合使用，可对道岔打受限区进行贯通打磨，显著提高岔区的动态平顺性。

曲面打磨车配备砂轮（最左侧为纸砂轮,其余为磨石砂轮）

曲面在工程学中有着广泛的作用，例如NURBS曲面在舰船垂向参数设计中具有重要的应用。首先通过NURBS曲面进行船体主尺度的计算，再利用NURBS曲面的控制点信息和三角面方程，通过约束条件得到船体各舱室的锤向参数以及结合船体曲面特征，然后对首位轮廓线控制点的参数和xxx横剖面的参数进行分析，通过研究能发现船体各舱室的重向参数之间存在几何上的耦合关系，结合上述方程式，垂向参数和横向线条曲线间的几何关系可通过NURBS曲面进行表达，因此可利用NURBS曲面生成船舶垂向参数曲面。

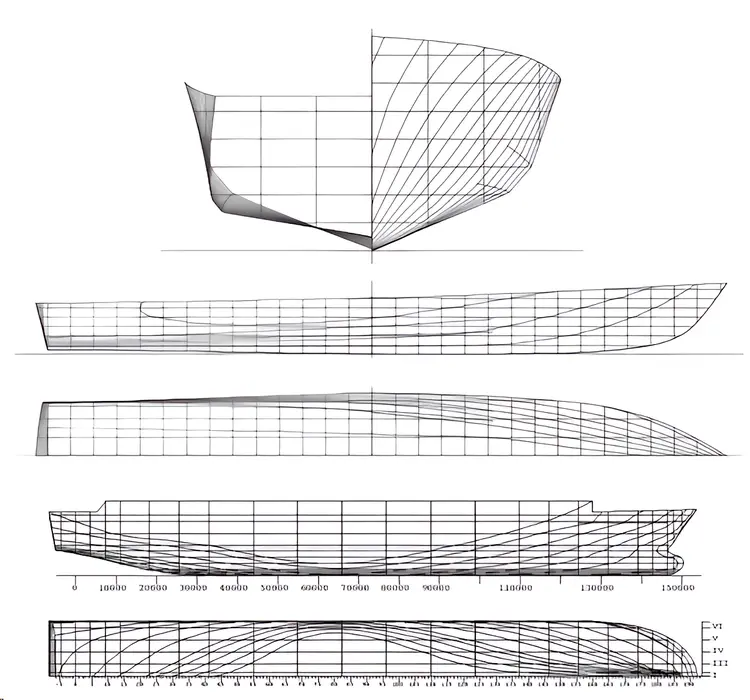
船体曲面特征线