星等

星等（英语：stellar magnitude）是天文学上对天体明暗程度的一种表示方法，用于区分天体亮度的等级。公元前2世纪，古希腊天文学家喜帕恰斯（Hipparchus）在编制星表时，将全天肉眼可见的恒星分为从1到6的6个等级，星等越小越明亮，由此用星等来表示恒星的亮度。19世纪，英国天文学家普森（N. R. Pogson）发现，传统上所定的1等星比6等星亮100倍，并用普森公式表示星等

除了地球的卫星月亮和太阳系几颗明亮的行星，肉眼可见的天体基本上都是恒星。恒星是自身可长期持续稳定发光的天体。对于肉眼观测者来说，直接观察到的恒星大部分位于银河系。星等就是天文学家对恒星或其他天体的亮度的度量。

早在公元前2世纪，古希腊天文学家喜帕恰斯（Hipparchus，旧译伊巴谷，又译依巴谷）在编制星表时发明了一种数字标度 ，来描述每颗恒星在天空中出现时的明亮程度。他将全天肉眼可见的恒星分成6个等级，最亮的定为1等星，最暗的定为6等星。一颗恒星的星等值越小，意味着看起来越明亮。天文学沿用了依巴谷标度的做法，用星等来表示恒星的亮度。 利用灵敏的探测器，天文学家可以测量天体的视星等，其精度达

星等，而星等差的精度达

星等。依巴谷标度法在亮和暗两个方向上都得到了扩展。

1850年，英国天文学家普森（N. R. Pogson）用光度计测量发现，习惯上所定的1等星比6等星亮100倍。普森采用下面的公式表示两颗星的星等与亮度之间的关系：

其中

，

分别定义为两颗星的视星等，

,

分别表示它们的亮度，即单位面积接收到的辐射流量。此处的亮度，指的是观测者所观察到的恒星亮度，并不是恒星本身的固有亮度，因此相应的星等称之为视星等。普森公式给出了联系两个天体的亮度与星等关系的表达式：

视星等是地球上或空间探测器观测到的天体亮度的一种度量。恒星的视星等反映出通过肉眼或天体辐射接收器所观测到的恒星亮度，它给出了天体的照度而不是光度。遥远的非常亮的高光度天体与近而弱的天体，可以有相同的视星等。

天体的光度（英语：luminosity）表示天体在所有波段上每秒钟所辐射出的总能量，一般用

表示。光度是恒星的本质属性，与观测者的运动方式和所在位置无关，它反映出恒星真正的发光强度。天体的亮度（英语：brightness）是对观察者而言。就像在一个很大的暗室中心点燃一支蜡烛，在距离蜡烛1m和100m的地方，对同一个观察者，他对后者的视觉感觉要暗得多。恒星的亮度定义为在观测点与星光垂直的平面上，星光产生的照度。照度（英语：illumination）主要体现发光体在某一距离

处单位面积上的光通量，天体物理中一般用

表示照度。照度的含义是“被照亮的程度"，单位是勒克斯(lx)。由于恒星的距离非常遥远，星光传到地球上，其照度非常微弱。因此恒星的亮度虽然以照度为定义，却不用勒克斯单位来描述。天体的照度

、发光强度

和到天体的距离

有以下关系

其中

表示天体单位立体角内的光照强度，故结合普森公式，视星等可表示为

除了太阳以外，其他恒星都离地球非常遥远。测量恒星的固有亮度与确定它们的距离密不可分。1761年出现了一次罕见的金星凌日现象，天文学家首次利用三角视差法，测量出了地球到金星的距离。三角视差法，即勘测人员常用的三角测量技术。例如，测量远处山峰的距离，可以通过两个不同观测点与山峰之间的夹角位量来确定。其中，这两个观测点之间的距离是已知的基线距离，然后使用三角法就能计算得出山峰的距离。同理，在地球上相距甚远的观测点，也可以测量出地球到行星的距离。测量恒星的距离，需要比地球直径更长的基线。当地球绕太阳公转时，相隔六个月观测同一颗恒星，所使用的基线正好等于地球公转轨道直径。通过测量视差角 𝑝（角位置xxx变化的一半），我们可以计算出到恒星的距离 𝑑。

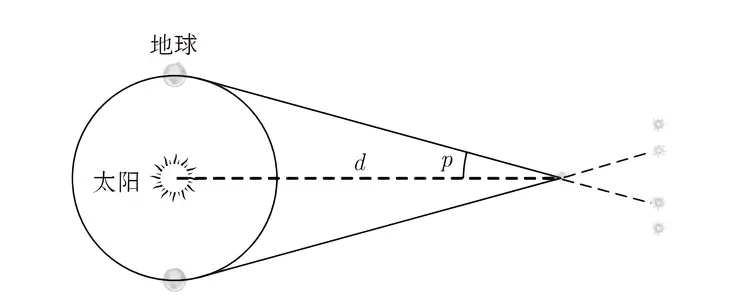图1 恒星视差

上式采用了小角度近似

，其中视差角

的单位是弧度（rad）。将

转换为以角秒（arc sec）为单位 ，并将视差角

时到该恒星的距离定义为1 pc（秒差距，parallax-second，缩写为pc），可以得到

1 pc 是地球轨道半径（1 AU）相对恒星与地球的连线张角为1“ 时，所对应的恒星距离。 三角视差法测定恒星距离的基本步骤包括：每隔半年拍摄数十张待测恒星及其背景星的照片或CCD图像，并对这些数据进行详细分析和计算。这种方法是测定恒星距离的最基础且最可靠的技术之一。由于越远的恒星视差越小，因此需要更高的观测精度。太阳之外，离我们最近的恒星是半人马座比邻星，其视差角为0.77”。从1989年到1993年，欧洲空间局 (ESA，简称欧空局）的依巴谷空间天体测量卫星在远离地球抖动的大气之上运行。该卫星能够测量的视差角的精度接近0.001"，它测量了超过118000颗恒星，对应的距离达到1000 pc。

光远离光源时，探测器接收到的辐射量即光源的视亮度，与其至光源距离的平方成反比。恒星的光度也会影响恒星的视亮度。恒星的视亮度与恒星的光度成正比，与其距离的平方成反比，即

两颗相同的恒星，当且仅当至地球的距离相同时，才具有相同的视亮度。恒星的亮度是根据探测器接收到的恒星辐射流量

来测定的。辐射流量是单位时间内与光传播方向垂直的单位接收面积

内，所有波长的光的总能量。从一个天体接收到的辐射流量，取决于该天体的固有光度以及它与观测者之间的距离。一颗光度为

的恒星，在距离

处测量到它的辐射流量

，可以表达为

上式的分母即球面积，由于光度

并不依赖于

，所以辐射流量

反比于距离

的平方。这就是光的平方反比定律。

由于历史原因，光学波段天体的分光流量密度不是用绝对单位，而是采用相对测量，即星等。利用平方反比定律，天文学家可以给恒星确定一个xxx星等

，定义为位于10 pc处天体的视星等。

天文学家研究恒星，最主要的信息源是来自恒星的电磁波辐射。在恒星辐射的全部电磁波中，可见光波段只占很窄的一段，却是迄今为止人类获取天体信息最多的一段。借助xxx星等可定义天体的光度。天体的光度测量，指的是测量天体的辐射流，由望远镜和辐射接收器完成。将待测天体的响应，与已知光度的天体或标准光源加以比较，可求出待测天体的光度。由于探测器都有选择性，因而有测光系统（如UBV系统）。继承历史上天文学家的发现，两颗恒星相差5个视星等，那么星等较小的恒星比星等较大的恒星看上去亮100倍，可以给出这两颗恒星的流量比为

两边取对数可得到另一种形式:

光的平方反比定律把恒星的固有属性（光度

和xxx星等

）与在某个距离处观测该恒星得到的测量值，包括辐射流量

和视星等

联系到一起。

通过合并光的平方反比定律表达式即式（2.1）与式（3.1），可以发现视星等

和xxx星等

与恒星距离

之间的联系：

其中，

是假如恒星在位于10 pc的距离处，我们可接收到的辐射流量；

是恒星的距离，以pc为单位。求解

，给出

由式（3.4）可以看出，视星等和xxx星等之差

是恒星距离的一个量度，天文学家称之为恒星的距离模数（英文：distance modulus），即

对于相同距离的两颗星，光的平方反比定律即式（2.1）表明，它们的辐射流量之比等于光度之比。因此，对于xxx星等有

假设其中一颗恒星是太阳，这揭示了恒星的xxx星等与它的光度之间的直接关系：

其中，太阳的xxx星等和光度分别为

和

W。

对恒星的光度进行测量，是了解恒星内部结构的重要手段之一。为了比较各天文台的观测结果，必须建立标准测光系统。最早提出的国际系统有仿视星等

和照相星等

。

恒星的光度测量，就是通过望远镜和辐射探测器测量恒星或其他天体的亮度，以及亮度的变化情况。辐射探测器是天文望远镜的附属设备，可以是照相底片、光电倍增管、电荷藕合器件(CCD)等。由于不同探测器有不同的分光灵敏度曲线，因此当谈到天体的亮度或星等时应注明星等系统，否则无意义。不同的测量方法或观测波段对同一天体可以给出不同的星等，这就产生了不同的星等系统或光度系统。人眼对黄绿光（平均波长约550 nm）最敏感，所观测到的星等称为目视星等，记为

；早期的照相底片对蓝紫光（250～500 nm，平均波长约为430 nm）最敏感，所测到的星等称为照相星等，记为

；用黄绿色滤光片配合照相底片，得到的与人眼灵敏度大致相同的仿视星等，记为

；此外，还有由安装在望远镜终端的光电光度计测得的光电星等；用对各个波段辐射灵敏度均相同的探测器测得的辐射星等；表征在整个电磁波段辐射总量的热星等。

光度对应的星等是xxx热星等系统，即用测热辐射计测量恒星的总辐射所得到的星等系统。辐射热计是一种仪器，用来测量它接收到的所有波长的辐射流量所引起的温度升高。如果视星等和xxx星等是对恒星发射的所有波长的光进行测量的结果，那么它们被称为热星等，并分别用

和

表示。然而，探测器只能在其灵敏度限定范围的特定波长区域内测量恒星的辐射流量。天体的辐射是多波段的，不同波段有不同的辐射强度。分别测量各个波段的辐射强度可以提供一些很重要的信息。分波段进行的光度测量称为分光光度测量。恒星的颜色可以通过使用只在某些窄波段内允许传输星光的滤光片来精确确定。1953年，美国天文学家约翰逊 (Harold Lester Johnson)和摩根（William Wilson Morgan）提出一种UBV三色国际星等系统，即通过加滤光片的方法，对每一颗恒星测量3个不同波段的亮度。在标准的UBV系统中，一颗恒星的视星等是通过三个滤光片来测量的，用三个大写字母表示它们：- U，恒星的紫外星等，是通过中心波长为 365 nm、有效带宽为68 nm的滤光片测量的。- B，恒星的蓝色星等，是通过中心波长为 440 nm、有效带宽为98 nm的滤光片测量的。- V，恒星的目视星等，是通过中心波长为 550 nm、有效带宽为89nm的滤光片测量的。天文学家斯特龙根（Bengt Georg Daniel Strömgren）提出的uvby测光系统属于中带测光系统，不同观测波段之间完全独立，而UBV系统是一种宽带测光系统，不同滤光片之间存在一定重叠。

常用测光系统不同波段的中心波长和带宽

星等值的获得，是先用天文仪器测定星的亮度，然后通过星等与亮度的换算公式计算出来。

色指数是同一天体在任意两个波段内的星等差（短波段星等减长波段星等），恒星的不同颜色是由恒星在不同光学波段上的强度不同引起的，因而同恒星的色指数和色温度密切相关。习惯上通用的色指数是款波段UBV测光系统中的

和

。利用式（3.5），如果已知恒星距离

，则可以确定恒星的颜色xxx星等

和

。恒星的

色指数是其紫外星等和蓝色星等的差值，而恒星的

色指数是其蓝色星等和目视星等之间的差值，即

和

恒星的星等值随亮度的增加而减小；结果是，色指数

更小的恒星，就比色指数

更大的恒星显得更蓝。因为色指数是两个星等的差值，所以式（3.5）表明它独立于恒星的距离。

热改正（BC，Bolometric Correction）是把目视星等换算成热星等所必须加的改正值。xxx热星等与xxx目星等之差被称为热改正BC，即

通过光谱方法测定了热改正，则恒星的热星等可以通过目视星等与热改正来计算求得。

星光穿过大气层，会受到大气分子、原子的吸收和散射而使强度减弱，称为大气消光。处在不同地平高度的恒星，星光穿过大气层的厚度不同，再加上大气密度的变化，大气消光的程度差异很大。星等数的确定应以改正过大气消光的星的亮度，即地球大气外的恒星亮度为依据。为了将星光产生的照度与用星等数表示的恒星亮度相联系，规定0等星在地球大气外的照度为

勒克斯。于是，星等数为

的恒星在大气外产生的照度为

值原本是测定的织女星的大气外照度，即认定织女星为标准0等星。但后来更精确的测量发现，织女星的大气外照度略低于

勒克斯。天文学家最终决定，固定

值不变，放弃以织女星为标准0等星的概念，重新认定织女星的视星等为0.03。无论用何种探测器进行光度测量，都有两个共同的问题：光度标准和大气消光改正问题。光度标准通常选用己精确知道其星等的定标星，而大气消光受天气、季节、天体的高度和当地大气质量等多种因素的影响，准确地加以改正是相当复杂而困难的。

天文学家通过研究恒星、星系及星际气体和尘埃云发出的光，并定量测量电磁波谱中的光强度和偏振，深入理解了太阳系以外的宇宙。星际物质的存在，对星光产生吸收和散射，使星光减弱，这种现象称为星际消光，消光量定义为

其中

为相应的波长，O和T分别代表观测值和真值。星际消光

与波长有以下关系

在光学波段，

，即

星光通过星际空间而变红的现象称为星际红化。为了表示星际红化，定义观测色指数与真实色指数之差为色余（Colour excess）。观测色指数大于真实色指数，即天体显红时，色余为正。正色余大都是星际红化引起的，星际尘埃对短波的消光作用大于对长波的消光作用。这时色余与光线穿过的距离成正比，因而可根据色余值来估计天体的距离。

天空中最亮的15颗恒星