什么是遗传算子
编辑遗传算子是一种操作者在使用遗传算法来引导算法朝解决给定问题。共有三种主要类型的算子(变异、交叉和选择),它们必须相互配合才能使算法成功。遗传算子用于创建和维护遗传多样性(变异算子),将现有解决方案(也称为染色体)组合成新解决方案(交叉)并在解决方案之间进行选择(选择)。在他的书中讨论了遗传编程的使用为了优化复杂问题,计算机科学家JohnKoza还确定了一个“反转”或“置换”算子;然而,这个算子的有效性从来没有被最终证明过,这个算子也很少被讨论。
变异(或类变异)算子被称为一元算子,因为它们一次只对一条染色体进行运算。相比之下,交叉算子被称为二元算子,因为它们一次对两条染色体进行操作,将两条现有的染色体组合成一条新的染色体。
操作员
编辑遗传变异是进化过程的必要条件。遗传算法中使用的遗传算子类似于自然界中的遗传算子:适者生存,或选择;繁殖(交叉,也称为重组);和突变。
选择
编辑选择算子优先考虑更好的解决方案(染色体),允许他们将他们的“基因”传递给下一代算法。在传递给交叉算子之前,使用某种形式的目标函数(在遗传算法中也称为“适应度函数”)确定最佳解决方案。存在不同的选择最佳解决方案的方法,例如,适应度比例选择和锦标赛选择;不同的方法可能会选择不同的解决方案作为“最佳”。选择算子也可以简单地将当前一代的最佳解决方案直接传递给下一代而不进行变异;这被称为精英主义或精英选择。
交叉
编辑交叉是采用一种以上的母体溶液(染色体)并从中产生子溶液的过程。通过重新组合部分好的解决方案,遗传算法更有可能创建更好的解决方案。与选择一样,有许多不同的方法可以组合父解,包括边缘重组算子(ERO)以及“剪切和拼接交叉”和“均匀交叉”方法。通常选择交叉方法来与解决方案的染色体表示紧密匹配;当变量组合在一起作为构建块时,这可能变得尤为重要,这可能会被不尊重的交叉操作员打断。同样,交叉方法可能特别适合某些问题;ERO通常被认为是解决旅行商问题的好选择。
突变
编辑变异算子鼓励解决方案之间的遗传多样性,并试图通过阻止解决方案变得过于接近来防止遗传算法收敛到局部最小值。在改变当前的解决方案池时,给定的解决方案可能与之前的解决方案完全不同。通过变异解,遗传算法可以仅通过变异算子达到改进的解。同样,可以使用不同的突变方法;这些范围从简单的位突变(以低概率翻转二进制字符串染色体中的随机位)到更复杂的突变方法,这些方法可以用从均匀分布或随机分布中选择的随机值替换解决方案中的基因。高斯分布。与交叉算子一样,通常选择变异方法来匹配染色体内解的表示。
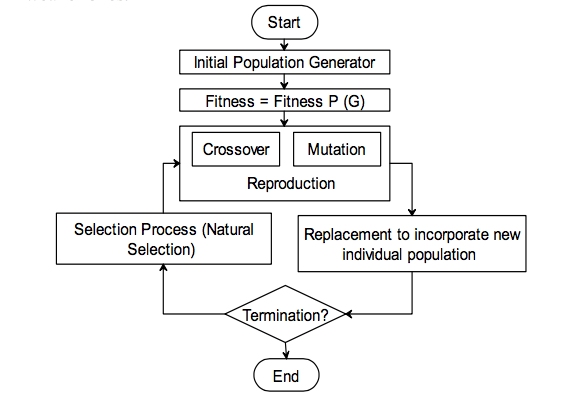
组合运算符
编辑虽然每个算子都用于改进由单独工作的遗传算法产生的解决方案,但这些算子必须相互协作才能使算法成功找到好的解决方案。单独使用选择运算符将倾向于用总体中最佳解决方案的副本填充解决方案总体。如果在没有变异算子的情况下使用选择和交叉算子,算法将趋于收敛到局部最小值,即问题的一个很好但次优的解决方案。单独使用变异算子会导致随机游走通过搜索空间。只有同时使用这三个算子,遗传算法才能成为一种耐噪声的爬山算法,从而为问题提供良好的解决方案。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/124829/
