离散余弦变换

离散余弦变换（DCT）表示的有限序列的数据点中的总和而言余弦函数在不同的振荡频率。DCT由NasirAhmed于1972年首次提出，是信号处理和数据压缩中广泛使用的转换技术。它用于大多数数字媒体，包括数字图像（如JPEG和HEIF，可以丢弃小的高频成分）、数字视频（如MPEG和H.26x）、数字音频（如DolbyDigital、MP3和AAC）、数字电视（如SDTV、HDTV和VOD）、数字广播（如AAC+和DAB+）和语音编码（如AAC-LD、Siren和Opus）。DCT对于科学和工程中的许多其他应用也很重要，例如数字信号处理、电信设备、减少网络带宽。偏微分方程数值解的用法和谱方法。

使用余弦而不是正弦函数对于压缩至关重要，因为事实证明（如下所述）逼近典型信号所需的余弦函数较少，而对于微分方程，余弦表示边界条件的特定选择。具体而言，离散余弦变换是一种类似于离散傅里叶变换(DFT)的傅里叶相关变换，但仅使用实数.DCT通常与周期性和对称扩展序列的傅立叶级数系数​​相关，而DFT仅与周期性扩展序列的傅立叶级数系数​​相关。离散余弦变换相当于长度大约两倍的DFT，对具有偶对称性的真实数据进行操作（因为实函数的傅立叶变换是实函数和偶函数），而在某些变体中，输入和/或输出数据被移动了一半一个样品。有八种标准DC​​T变体，其中四种是常见的。

离散余弦变换最常见的变体是II型DCT，通常简称为“DCT”。这是由Ahmed首次提出的原始DCT。它的逆，III型DCT，相应地通常简称为“逆DCT”或“IDCT”。两个相关的变换是离散正弦变换(DST)，它等效于实函数和奇函数的DFT，以及改进的离散余弦变换(MDCT)，它基于重叠的DCT数据。开发了多维DCT(MDDCT)以将DCT的概念扩展到MD信号。有几种算法可以计算MDDCT。已经开发了多种快速算法来降低实现DCT的计算复杂度。其中之一是整数离散余弦变换(IntDCT)，它是标准DC​​T的整数近似值，用于多个ISO/IEC和ITU-T国际标准。

离散余弦变换压缩，也称为块压缩，以离散DCT块组的形式压缩数据。DCT块可以有多种尺寸，包括标准DC​​T的8x8像素，以及4x4和32x32像素之间的各种整数DCT尺寸。离散余弦变换具有很强的“能量压缩”特性，能够在高数据压缩率下实现高质量。但是，当应用大量DCT压缩时，会出现块状压缩伪影。

离散余弦变换是信号处理中使用最广泛的变换技术，也是迄今为止数据压缩中使用最广泛的线性变换。未压缩的数字媒体以及无损压缩具有不切实际的高内存和带宽要求，而高效的DCT有损压缩技术显着降低了这一要求，能够实现从8:1到14的数据压缩比:1表示接近工作室质量，最高100:1表示可接受质量的内容。离散余弦变换压缩标准用于数字媒体技术，如数字图像、数字照片、数字视频、流媒体、数字电视、流媒体电视、视频点播(VOD)、数字影院、高清视频(HDvideo)和高清电视(HDTV)。

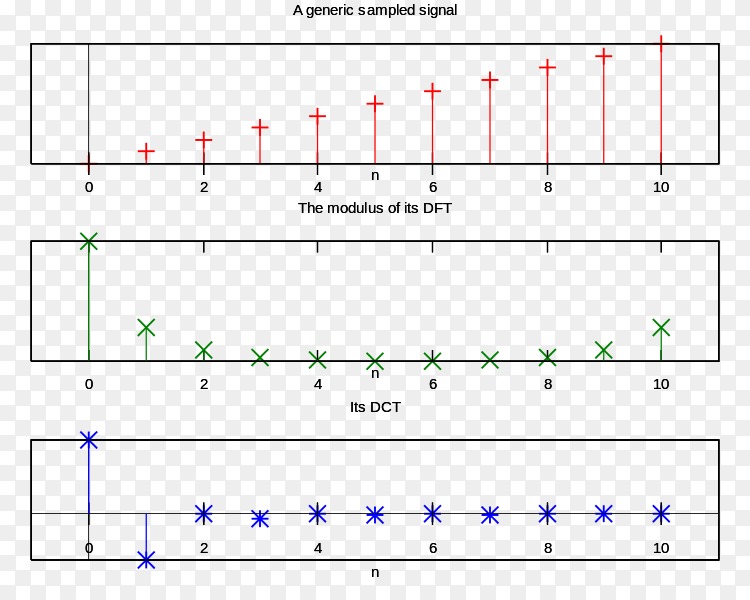
离散余弦变换，尤其是DCT-II，经常用于信号和图像处理，尤其是有损压缩，因为它具有很强的“能量压缩”特性：在典型应用中，大部分信号信息往往集中在DCT的几个低频分量中。对于强相关的马尔可夫过程，DCT可以接近Karhunen-Loève变换的压缩效率（在去相关意义上是最佳的）。如下所述，这源于余弦函数中隐含的边界条件。

离散余弦变换还广泛用于通过谱方法求解偏微分方程，其中DCT的不同变体对应于阵列两端略有不同的偶/奇边界条件。

离散余弦变换也密切相关的切比雪夫多项式，并快速DCT算法（下文）中，使用切比雪夫逼近由一系列Chebyshev多项式的任意的功能，例如在Clenshaw-柯蒂斯正交。

离散余弦变换是多媒体电信设备的编码标准。它被广泛用于降低比特率，减少网络带宽使用。DCT压缩显着减少了数字信号所需的内存量和带宽。