排序算法

在计算机科学中，排序算法是一种将列表元素按顺序排列的算法。最常用的顺序是数字顺序和字典顺序，以及升序或降序。高效排序对于优化要求输入数据在排序列表中的其他算法（例如搜索和合并算法）的效率很重要。排序对于规范化数据和产生人类可读的输出通常也很有用。

形式上，任何排序算法的输出必须满足两个条件：

1. 输出是单调顺序的（每个元素不小于/大于前一个元素，根据所需的顺序）。
2. 输出是输入的排列（重新排序，但保留所有原始元素）。

为了获得最佳效率，输入数据应存储在允许随机访问的数据结构中，而不是只允许顺序访问的数据结构中。

从计算开始，排序问题就吸引了大量的研究，这可能是由于尽管它简单、熟悉的陈述，但有效解决它的复杂性。1951年左右早期排序算法的作者之一是从事ENIAC和UNIVAC工作的BettyHolberton。早在1956年就对冒泡排序进行了分析。自20世纪中叶以来，渐近最优算法就已为人所知——新算法仍在被发明，广泛使用的Timsort可追溯到2002年，而库sort于2006年首次发布。

比较排序算法具有Ω(nlogn)比较的基本要求（某些输入序列将需要nlogn比较的倍数，其中n是要排序的数组中的元素数）。不基于比较的算法，例如计数排序，可以有更好的性能。

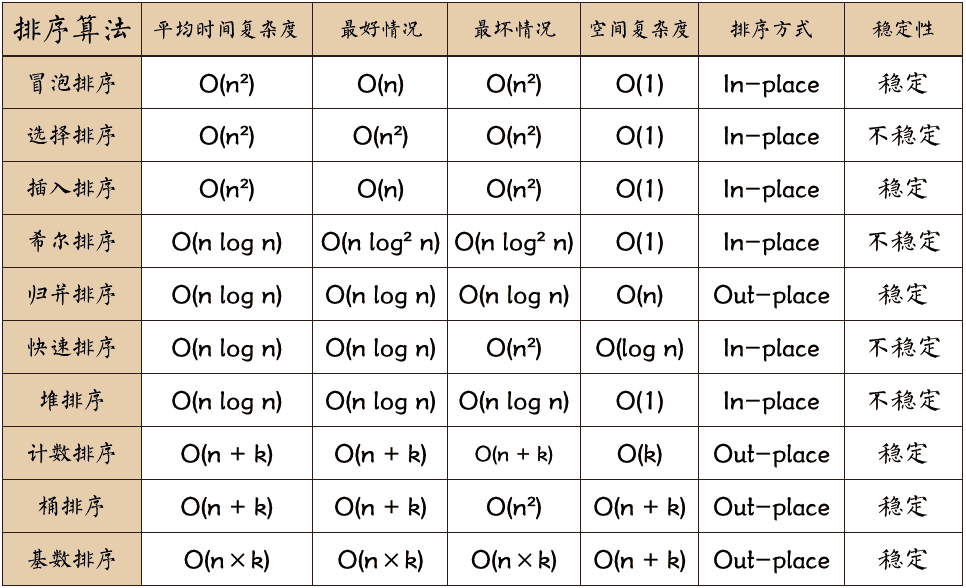
排序算法在计算机科学入门课程中很流行，针对该问题的大量算法提供了对各种核心算法概念的温和介绍，例如大O表示法、分治算法、堆和二叉树等数据结构、随机算法、最佳、最差和平均情况分析、时空权衡以及上下限。

以最佳方式（以最少的比较和交换）或快速（即考虑机器特定的细节）对小数组进行排序仍然是一个开放的研究问题，只有非常小的数组（<20个元素）才知道解决方案。在并行机器上进行类似的最优（根据各种定义）排序是一个开放的研究课题。

排序算法可以分为：

• 计算复杂度
  • 就列表大小而言的最佳、最差和平均情况行为。对于典型的串行排序算法，好的行为是O(nlogn)，并行排序是O(log2n)，不好的行为是O(n2)。串行排序的理想行为是O(n)，但在一般情况下这是不可能的。最佳并行排序为O(logn)。
  • 交换“就地”算法。
• 内存使用（以及其他计算机资源的使用）。特别是，一些排序算法是“就地”的。严格来说，就地排序只需要O(1)内存，而不是被排序的项目；有时O(logn)额外内存被认为是“就地”。
• 递归：一些算法要么是递归的，要么是非递归的，而另一些可能两者兼而有之（例如，归并排序）。
• 稳定性：稳定的排序算法保持具有相等键（即值）的记录的相对顺序。
• 它们是否是比较排序。比较排序仅通过使用比较运算符比较两个元素来检查数据。
• 一般方法：插入、交换、选择、合并等。交换排序包括冒泡排序和快速排序。选择排序包括循环排序和堆排序。
• 算法是串行的还是并行的。本讨论的其余部分几乎完全集中于串行算法并假设串行操作。
• 适应性：输入的预排序是否影响运行时间。考虑到这一点的算法已知是自适应的。
• 在线：在线的插入排序等算法可以对恒定的输入流进行排序。

稳定的排序算法按照它们在输入中出现的相同顺序对相等的元素进行排序。例如，在右侧的卡片排序示例中，卡片按其等级排序，而它们的花色被忽略。这允许原始列表的多个不同正确排序版本的可能性。稳定的排序算法选择其中之一，根据以下规则：如果两个项目比较相等（如两张5卡），则它们的相对顺序将被保留，即如果输入中一个在另一个之前，它将来在输出中的另一个之前。

稳定性对于保持同一数据集上多个排序的顺序很重要。例如，假设由姓名和班级部分组成的学生记录是动态排序的，首先按姓名，然后按班级部分。如果在这两种情况下都使用稳定的排序算法，则sort-by-class-section操作不会改变名称顺序；对于不稳定的排序，可能是按部分排序会打乱姓名顺序，从而导致学生列表不按字母顺序排列。

更正式地说，被排序的数据可以表示为值的记录或元组，用于排序的数据部分称为键。在卡片示例中，卡片表示为记录（等级、花色），键是等级。一个排序算法是稳定的，如果有两个记录R和S具有相同的键，并且R在原始列表中出现在S之前，那么R在排序列表中总是出现在S之前。

当相等的元素无法区分时，例如整数，或更一般地说，任何以整个元素为关键的数据，稳定性都不是问题。如果所有键都不同，稳定性也不是问题。

不稳定的排序算法可以专门实现稳定。这样做的一种方法是人为地扩展键比较，以便使用原始输入列表中条目的顺序作为决胜局来决定具有其他相同键的两个对象之间的比较。然而，记住这个顺序可能需要额外的时间和空间。

虽然有大量的排序算法，但在实际实现中，少数算法占主导地位。插入排序广泛用于小数据集，而对于大数据集，则使用渐近有效的排序，主要是堆排序、归并排序或快速排序。高效的实现通常使用混合算法，将整体排序的渐近高效算法与递归底部的小列表的插入排序相结合。高度调整的实现使用更复杂的变体，例如在Android、Java和Python中使用的Timsort（合并排序、插入排序和附加逻辑），以及在某些C++排序中（以变体形式）使用的introsort（快速排序和堆排序）实现和.NET。

对于更受限的数据，例如固定区间的数字，广泛使用计数排序或基数排序等分布排序。冒泡排序和变体在实践中很少使用，但在教学和理论讨论中很常见。

在对对象进行物理排序时（例如按字母顺序排列的论文、测试或书籍），人们直观地通常对小集合使用插入排序。对于较大的集合，人们通常首先进行分组，例如按首字母，并且多个分组允许对非常大的集合进行实际排序。通常空间相对便宜，例如将物体散布在地板上或大面积上，但操作成本高，尤其是移动物体很远的距离——参考的位置很重要。合并排序对于物理对象也很实用，特别是因为可以使用两只手，每个要合并的列表一只手，而其他算法，例如堆排序或快速排序，不适合人类使用。其他算法，如库排序，一种保留空格的插入排序的变体，对于物理使用也很实用。

最简单的两种排序是插入排序和选择排序，由于开销低，这两种排序在小数据上都很有效，但在大数据上效率不高。插入排序在实践中通常比选择排序快，因为在几乎排序的数据上比较少和性能好，因此在实践中是首选，但选择排序使用较少的写入，因此在写入性能是一个限制因素时使用。

插入排序是一种简单的排序算法，对于小型列表和大多数已排序的列表相对有效，并且通常用作更复杂算法的一部分。它的工作原理是从列表中一个一个地取出元素，并将它们插入到一个新的排序列表中的正确位置，类似于我们将钱存入钱包的方式。在数组中，新列表和剩余的元素可以共享数组的空间，但是插入是昂贵的，需要将所有后续元素移动一个。Shellsort（见下文）是插入排序的一种变体，对于较大的列表更有效。

选择排序是一种就地比较排序。它具有O(n2)复杂度，使其在大型列表上效率低下，并且通常比类似的插入排序表现更差。选择排序以其简单性着称，在某些情况下也比更复杂的算法具有性能优势。

该算法找到最小值，将其与xxx个位置的值交换，然后对列表的其余部分重复这些步骤。它不超过n次交换，因此在交换非常昂贵的情况下很有用。

实用的通用排序算法几乎总是基于平均时间复杂度（通常是最坏情况复杂度）O(nlogn)的算法，其中最常见的是堆排序、归并排序和快速排序。每个人都有优点和缺点，最显著那么简单实现合并排序使用O（ñ）额外的空间，并实现简单快速排序为O（ñ2）最坏情况的复杂性。这些问题可以以更复杂的算法为代价来解决或改善。

虽然这些算法在随机数据上是渐近有效的，但为了在现实世界数据上的实际效率，使用了各种修改。首先，这些算法的开销在较小的数据上变得显着，因此通常使用混合算法，一旦数据足够小，通常会切换到插入排序。其次，算法通常在已经排序的数据或几乎排序的数据上表现不佳——这些在现实世界的数据中很常见，并且可以通过适当的算法在O(n)时间内排序。最后，它们也可能是不稳定的，而稳定性通常是一种理想的属性。因此，通常会使用更复杂的算法，例如Timsort（基于归并排序）或introsort（基于快速排序，回退到堆排序）。