语言方程

语言方程是类似于数字方程的数学语句，但变量承担的是形式语言的值而不是数字。代替数字方程中的算术运算，变量是由语言运算连接的。在两种语言A和B上最常见的运算是集合并集A∪B，集合交集A∩B，以及串联A⋅B。最后，作为采取单一操作数的操作，集合A*表示语言A的Kleene星。因此，语言方程可以用来表示形式化语法，因为由语法生成的语言必须是语言方程系统的解。语言方程和无语境语法Ginsburg和Rice用语言方程给出了无语境语法的另一种定义。对于每个无语境语法g=(v,σ,r,s){displaystyleG=(V,Sigma,R,S)}，都与一个方程组相关。都有一个变量方程组。{displaystyleX=L_{G}(X)}是这个系统的最小解。是这个系统的最小解，也就是说，任何其他解都必须是这个解的子集。带有附加交集的语言方程类似地对应于共轭语法。语言方程和有限自动机Brzozowski和Leiss研究了左边的语言方程，其中每个连接都是与左边的单子常数语言相连接的，例如右手边有一个变量。每一个非确定性有限自动机都有这样的对应方程，使用左卡顿和联合，见图1。如果允许交叉操作，方程对应于交替的有限自动机。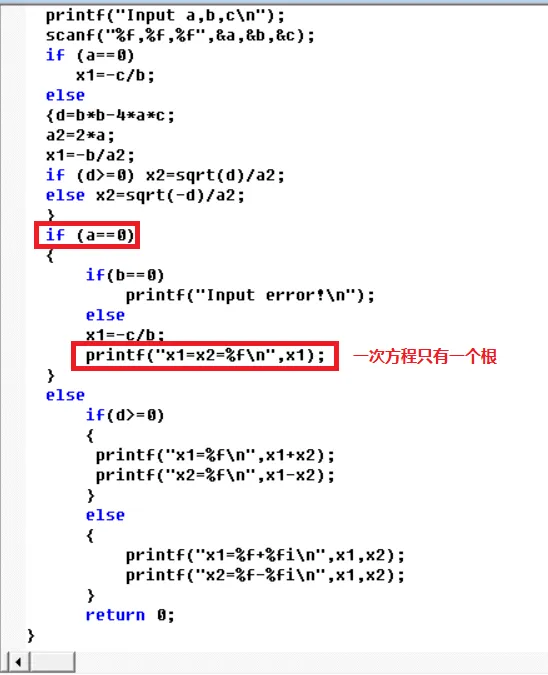

并证明他们的可满足性问题是EXPTIME-complete的。Conway的问题Conway提出了以下问题：给定一个恒定的有限语言L{displaystyleL}，方程的xxx解是什么？，是方程的xxx解LX=XL{displaystyleLX=XL}总是有规律的吗？Karhumäki和Petre研究了这个问题，他们在一个特殊情况下给出了肯定的答案。昆克对康威的问题给出了一个强烈的否定答案，他构建了一个有限语言L{displaystyleL}这样，这个方程的xxx解就不是可递归列举的。Kunc还证明，不等式的xxx解是LX⊆XL{displaystyleLXsubseteqXL}的xxx解总是有规律的。总是有规律的。

带有连接和布尔运算的语言方程首先由Parikh,Chandra,Halpern和Meyer研究，他们证明了给定方程的可满足性问题是不可判定的，如果一个语言方程系统有一个xxx的解，那么这个解是递归的。后来，Okhotin证明了不可满足性问题是不完全的，每个递归语言都是某个方程的xxx解。

对于一个字母表，Leiss发现了xxx个具有非规则解的语言方程，使用了补数和连接操作。后来，Jeż表明，非规则单数语言可以通过语言方程的并集、交集和联集来定义，等同于共轭语法。通过这种方法，Jeż和Okhotin证明每个递归单数语言都是某个方程的xxx解。