SAT解算器

SAT解算器在计算机科学和形式化方法中，SAT解算器是一个旨在解决布尔可满足性问题的计算机程序。在输入一个布尔变量的公式时，比如（x或y）和（x或不y），SAT求解器会输出该公式是否可满足，即x和y有可能使该公式为真，或者不可满足，即x和y没有这种值。自从20世纪60年代引入SAT算法以来，现代SAT求解器已经发展成为复杂的软件产品，涉及到大量的启发式算法和程序优化，以便高效工作。根据一个被称为库克-列文定理的结果，布尔可满足性一般是一个NP-完全的问题。因此，只有指数级的最坏情况下的复杂度的算法是已知的。尽管如此，高效和可扩展的SAT算法在2000年代被开发出来，并且在我们自动解决涉及数万个变量和数百万个约束条件的问题实例的能力方面取得了巨大的进步。SAT求解器通常从将公式转换为共轭正常形式开始。它们通常基于核心算法，如DPLL算法，但也包括一些扩展和功能。大多数SAT求解器包括超时，所以即使他们不能找到一个输出为未知的解决方案，他们也会在合理的时间内终止。通常情况下，SAT求解器不只是提供一个答案，而是可以提供进一步的信息，包括在公式可满足的情况下提供一个赋值的例子（x，y等的值），或者在公式不可满足的情况下提供最小的不可满足的条款集。现代SAT求解器对包括软件验证、程序分析、约束条件求解、人工智能、电子设计自动化和运筹学等领域产生了重大影响。强大的求解器很容易以免费和开源软件的形式出现，并且被内置到一些编程语言中，比如在约束逻辑编程中把SAT求解器暴露为约束条件。概述DPLL求解器DPLLSAT求解器采用一个系统的回溯搜索程序来探索变量赋值的（指数大小）空间，寻找满意的赋值。这个基本的搜索过程是在20世纪60年代初的两篇开创性的论文中提出的,现在通常被称为Davis-Putnam-Logemann-Loveland算法（DPLL或DLL）。许多现代的实际SAT解题方法都是从DPLL算法中衍生出来的，并且具有相同的结构。通常他们只提高了某些类别的SAT问题的效率，如工业应用中出现的实例或随机生成的实例。

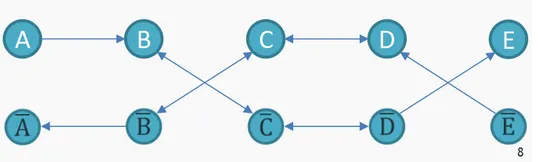
理论上，DPLL系列算法的指数下限已经被证明。不属于DPLL系列的算法包括随机的局部搜索算法。一个例子是WalkSAT。随机方法试图找到一个满意的解释，但不能推断出一个SAT实例是不可满足的，与完整算法相反，如DPLL。相比之下，随机算法，如Paturi,Pudlak,Saks和Zane的PPSZ算法，根据一些启发式方法，例如有界宽度解析，以随机顺序设置变量。如果启发式方法不能找到正确的设置，变量就会被随机分配。PPSZ算法的运行时间为为3-SAT。这是这个问题最有名的运行时间，直到2019年，Hansen、Kaplan、Zamir和Zwick发表了该算法的修改，运行时间为对于3-SAT，后者是目前已知的在所有k值下最快的k-SAT算法。后者是目前已知的k-SAT在所有k值下最快的算法。在有许多满足的赋值的情况下，Schöning的随机算法有更好的约束。

现代SAT求解器（2000年开发）有两种类型：冲突驱动型和前瞻型。这两种方法都是由DPLL演变而来。冲突驱动的求解器，比如冲突驱动的子句学习（CDCL），用高效的冲突分析、子句学习、非同步回溯（又称回跳），以及双打字单元传播、自适应分支和随机重启来增强基本的DPLL搜索算法。经验表明，这些基本的系统搜索的附加功能对于处理电子设计自动化（EDA）中出现的大型SAT实例至关重要。著名的实现包括Chaff和GRASP。前瞻性求解器特别加强了还原（超越了单元句传播）和启发式求解器，它们在困难实例上通常比冲突驱动的求解器更强（而冲突驱动的求解器在大实例上会好得多，因为这些实例内部实际上有一个简单的实例）。