蒙特卡洛方法

蒙特卡洛方法，或称蒙特卡洛实验，是一类广泛的计算算法，依靠重复随机抽样来获得数值结果。其基本概念是利用随机性来解决原则上可能是确定性的问题。它们经常用于物理和数学问题，在难以或无法使用其他方法时最为有用。蒙特卡洛方法主要用于三类问题：优化、数字积分和从概率分布中生成抽样。在与物理有关的问题中，蒙特卡洛方法对模拟具有许多耦合自由度的系统很有用，如流体、无序材料、强耦合固体和细胞结构。其他例子包括对输入有重大不确定性的现象进行建模，如商业中的风险计算，以及在数学中，对具有复杂边界条件的多维定积分的评估。在应用于系统工程问题上（太空、石油勘探、飞机设计等），基于蒙特卡洛的失败、成本超支和进度超支的预测通常比人类的直觉或其他软方法更好。原则上，蒙特卡洛方法可以用来解决任何具有概率解释的问题。根据大数法则，一些随机变量的预期值所描述的积分可以通过取该变量的独立样本的经验平均值（又称"样本平均值"）来近似。当变量的概率分布被参数化时，数学家经常使用马尔科夫链蒙特卡洛（MCMC）采样器。

根据遍历定理，静止分布是由MCMC采样器的随机状态的经验度量来近似的。在其他问题中，目标是从满足非线性进化方程的概率分布序列中生成抽样。这些概率分布流总是可以被解释为马尔科夫过程的随机状态的分布，其过渡概率取决于当前随机状态的分布。在其他情况下，我们得到的是采样复杂程度越来越高的概率分布流。这些模型也可以被看作是非线性马尔可夫链的随机状态的演变规律。模拟这些复杂的非线性马尔可夫过程的自然方法是对该过程的多个副本进行采样，在演化方程中用采样的经验度量代替随机状态的未知分布。与传统的蒙特卡洛和MCMC方法相反，这些均值场粒子技术依赖于连续的相互作用的样本。

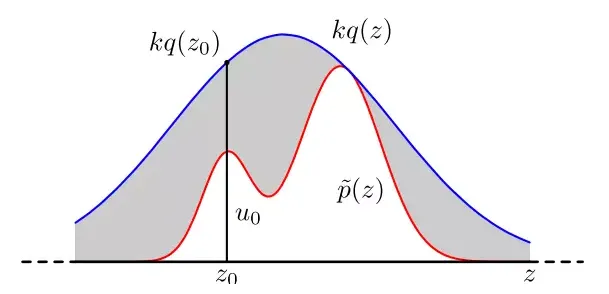
术语平均场反映了这样一个事实：每个样本（又称粒子、个体、步行者、代理、生物或表型）都与过程的经验度量相互作用。当系统的规模趋于无限大时，这些随机的经验度量就会收敛到非线性马尔可夫链的随机状态的确定性分布，这样，粒子之间的统计互动就消失了。尽管其概念和算法简单，但与蒙特卡洛模拟相关的计算成本可能高得惊人。一般来说，该方法需要许多样本才能得到一个好的近似值，如果单个样本的处理时间很高，可能会产生一个任意大的总运行时间。尽管在非常复杂的问题中这是一个严重的限制，但算法令人尴尬的并行性使得这种巨大的成本可以通过本地处理器、集群、云计算、GPU、FPGA等的并行计算策略来降低（也许是可行的水平）。

蒙特卡洛方法各不相同，但往往遵循一个特定的模式。

从该域的概率分布中随机产生输入对输入进行确定性的计算汇总结果例如，考虑一个象限（圆形区域）刻在一个单位正方形中。鉴于它们的面积之比为π/4，π的值可以用蒙特卡洛方法进行近似计算。