相位齐性

相位齐性是计算机图像中特征重要性的一种测量方法，是一种对照度和对比度变化特别稳健的边缘检测方法。

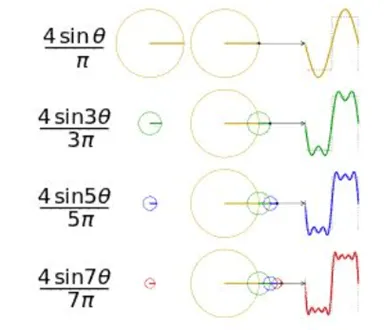
相位一致性反映了图像在频域中的行为。人们注意到，边缘特征的许多频率成分处于相同的相位。这个概念与相干性相似，只是它适用于不同波长的函数。例如，方波的傅里叶分解由正弦函数组成，其频率是基本频率的奇数倍。在方波的上升边缘，每个正弦分量都有一个上升相位；相位在边缘具有xxx的一致性。这对应于人类所感知的图像的边缘，那里有明暗之间的尖锐变化。

相位一致比较了信号的傅里叶分量的加权排列的傅里叶分量的加权排列。与傅里叶分量的总和。已经开发了几种实现相位一致的方法。考虑到用于其表述的不同符号，最近提出了一个统一的版本，其中还提出了一个参数调整的方法。

方波的例子很天真，因为大多数边缘检测方法都能很好地处理它。例如，xxx导数在边缘有一个xxx的量级。然而，在有些情况下，感知到的边缘并没有一个尖锐的阶梯或大的导数。相位一致的方法适用于许多其他方法失败的情况。一个明显的例子是由一条线组成的图像特征，如字母l。许多边缘检测算法会发现两个相邻的边缘：从白色到黑色，以及从黑色到白色的过渡。另一方面，相位一致图有一条线。这种情况的一个简单的傅立叶类比是一个三角波。在它的每个波峰中，都有一个来自不同正弦函数的波峰的同调。

计算图像的相位一致性图是非常密集的计算，而且对图像噪声很敏感。降噪技术通常在计算之前应用。