率失真理论

率损失理论是信息论的一个主要分支，为有损数据压缩提供了理论基础； 它解决了确定每个符号的最小位数的问题，以速率 R 衡量，应该通过信道进行通信，以便可以在接收器（输出信号）处近似地重建源（输入信号）而不超过预期失真D。

率损失理论给出了使用有损压缩方法可以实现多少压缩的分析表达式。许多现有的音频、语音、图像和视频压缩技术都具有变换、量化和比特率分配程序，这些程序利用了率失真函数的一般形状。

率失真理论是由克劳德香农在他的信息论基础工作中创建的。

在率失真理论中，率通常被理解为每个要存储或传输的数据样本的位数。失真的概念是一个持续讨论的主题。在最简单的情况下（大多数情况下实际使用），失真被定义为输入和输出信号之差的平方的期望值（即均方误差）。然而，由于我们知道大多数有损压缩技术对人类消费者（听音乐、看图片和视频）将感知到的数据进行操作，所以失真测量xxx以人类感知和美学为模型：很像概率的使用在无损压缩中，失真度量最终可以用贝叶斯估计和决策理论中使用的损失函数来识别。

在音频压缩中，感知模型（以及由此产生的感知失真测量）发展得相对较好，并经常用于 MP3 或 Vorbis 等压缩技术，但通常不容易包含在率失真理论中。在图像和视频压缩中，人类感知模型还不太成熟，包含的内容主要限于 JPEG 和 MPEG 加权（量化、归一化）矩阵。

失真函数测量用近似符号 x ^ {\displaystyle {\hat {x}}} 表示符号 x {\displaystyle x} 的成本。典型的失真函数是汉明失真和平方误差失真。

找到与速率和失真相关的函数作为以下最小化问题的解：

inf Q Y ‖ X ( y ‖ x ) I Q ( Y ; X ) 服从 D Q ≤ D ∗ 。 {\displaystyle \inf _{Q_{Y\mid X}(y\mid x)}I_{Q}(Y;X){\text{ subject to }}D_{Q}\leq D{*}.}

这里 Q Y ‖ X ( y ‖ x ) {\displaystyle Q_{Y\mid X}(y\mid x)} 有时称为测试通道，是通信通道输出的条件概率密度函数（PDF） （压缩信号）Y {\displaystyle Y} 对于给定的输入（原始信号）X {\displaystyle X} 和 I Q ( Y ; X ) {\displaystyle I_{Q}(Y;X)} 是 Y {\displaystyle Y} 和 X {\displaystyle X} 之间的互信息定义为

I ( Y ; X ) = H ( Y ) − H ( Y ∠ X ) {\displaystyle I(Y;X)=H(Y)-H(Y\mid X)\,}

其中 H ( Y ) {\displaystyle H(Y)} 和 H ( Y ∩ X ) {\displaystyle H(Y\mid X)} 是输出信号 Y 的熵和输出信号的条件熵给定输入信号

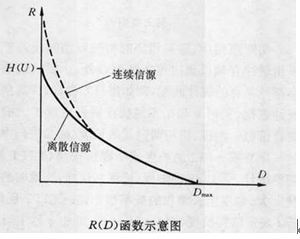
该问题也可以表述为失真率函数，我们在其中找到给定速率约束下可实现的失真的下限。

这两个公式导致函数互为反函数。

互信息可以理解为接收方对发送方信号 (H(Y)) 的“先验”不确定性的度量，该不确定性被接收到发送方信号信息后留下的不确定性所削弱 ( H ( Y ∩ X ) {\displaystyle H(Y\mid X)} )。 当然，不确定性的减少是由于信息量的交流，即 I ( Y ; X ) {\displaystyle I\left(Y;X。