后缀树

在计算机科学中，后缀树（也称为 PAT 树或更早的形式，位置树）是一种压缩的特里树，包含给定文本的所有后缀作为它们的键和文本中的位置作为它们的值。 后缩树允许特别快速地实现许多重要的字符串操作。

为字符串 S {\displaystyle S} 构建这样一棵树需要时间和空间与 S {\displaystyle S} 的长度成线性关系。 一旦构造完成，可以快速执行多个操作，例如在 S {\displaystyle S} 中定位子串，如果允许一定数量的错误则定位子串，定位匹配正则表达式模式等。后缩树还提供 最长公共子串问题的xxx个线性时间解决方案之一。 这些加速是有代价的：存储字符串的后缀树通常比存储字符串本身需要更多的空间。

McCreight (1976) 是xxx个为 S {\displaystyle S} 的所有后缀构建（压缩）特里树的人。 虽然以 i {\displaystyle i} 开始的后缀通常比前缀标识符长，但它们在压缩的 trie 中的路径表示在大小上没有差异。 另一方面，McCreight 可以免除 Weiner 的大部分辅助数据结构； 仅保留后缀链接。

Ukkonen (1995) 进一步简化了结构。 他提供了xxx个后缀树的在线构造，现在称为 Ukkonen 算法，其运行时间与当时最快的算法相匹配。这些算法对于恒定大小的字母表都是线性时间的，并且具有最坏情况的运行 通常 O ( n log ⁡ n ) {\displaystyle O(n\log n)} 的时间。

Farach (1997) 给出了xxx个对所有字母都最优的后缀树构造算法。 特别是，这是xxx个线性时间算法，用于从多项式范围内的整数字母表中提取的字符串。 Farach 的算法已成为构建后缀树和后缀数组的新算法的基础，例如，在外部存储器、压缩、简洁等中。

长度为 n {\displaystyle n} 的字符串 S {\displaystyle S} 的后缀树被定义为这样一棵树：

• 这棵树正好有 n 片叶子，编号从 1 {\displaystyle 1} 到 n {\displaystyle n} 。
• 除根节点外，每个内部节点至少有两个子节点。
• 每条边都标有 S {\displaystyle S} 的非空子串。
• 从一个节点开始的两条边不能有以相同字符开头的字符串标签。
• 通过连接从根到叶 i {\displaystyle i} 路径上找到的所有字符串标签获得的字符串拼出后缀 S [ i 。 . n ] {\displaystyle S[i..n]} ，因为 i {\displaystyle i} 从 1 {\displaystyle 1} 到 n {\displaystyle n} 。

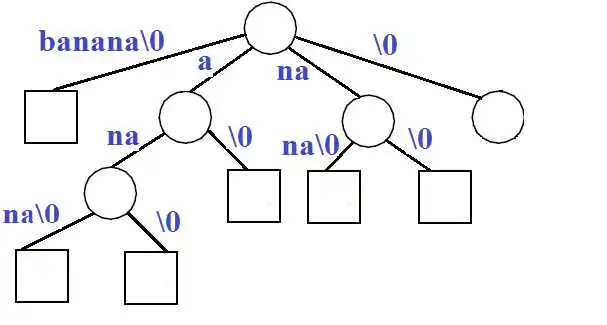
由于并非所有字符串都存在这样的树，因此 S {\displaystyle S} 被填充了一个在字符串中看不到的终端符号（通常表示为 $）。 这确保没有后缀是另一个后缀的前缀，并且将有 n {\displaystyle n} 个叶节点，一个对应于 S {\displaystyle S} 的 n {\displaystyle n} 个后缀中的每一个。 由于所有内部非根节点都是分支的，因此最多可以有 n − 1 个这样的节点，并且总共有 n + (n − 1) + 1 = 2n 个节点（n 个叶子，n - 1 个内部非根节点，1 根）。

后缀链接是较旧的线性时间构建算法的关键特征，尽管大多数基于 Farach 算法的较新算法都省去了后缀链接。