位移电流

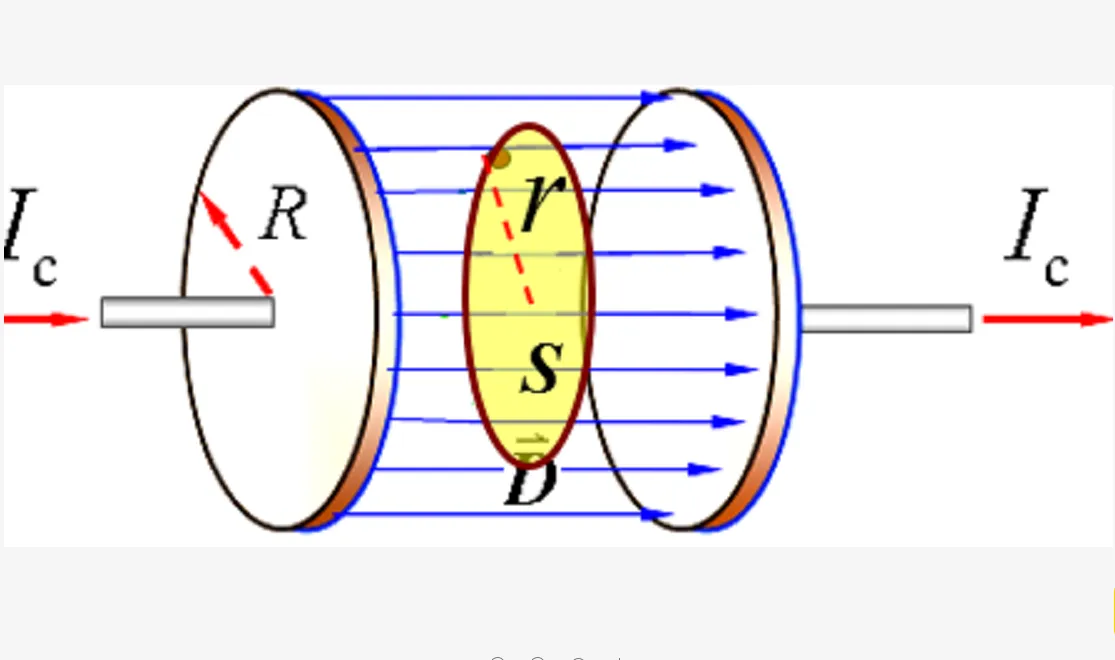
在电磁学中，位移电流密度是出现在麦克斯韦方程组中的量 ∂D/∂t，它根据电位移场 D 的变化率定义。 位移电流密度与电流密度的单位相同，与实际电流一样是磁场的来源。 然而，它不是移动电荷的电流，而是时变电场。 在物理材料中（与真空相反），原子中电荷的轻微运动也有贡献，称为介电极化。

位移电流项现在被视为完成麦克斯韦方程组的重要补充，并且是解释许多现象所必需的，尤其是电磁波的存在。

在哪里：

• ε0为自由空间的介电常数；
• E为电场强度； 和
• P 是介质的偏振。

对这个方程对时间进行微分定义了位移电流密度，因此它在电介质中有两个分量：（另请参见文章电流密度的位移电流部分）

右边的xxx项存在于物质媒体和自由空间中。 它不一定来自任何实际的电荷运动，但它确实有一个相关的磁场，就像电流由于电荷运动而产生的一样。 一些作者将名称位移电流单独应用于xxx项。

右侧的第二项称为极化电流密度，来自介电材料单个分子的极化变化。 当在外加电场的影响下，分子中的电荷从完全抵消的位置移动时，就会产生极化。 分子中的正电荷和负电荷分开，导致极化状态 P 增加。极化状态的变化对应于电荷运动，因此相当于电流，因此称为极化电流。

这种极化是麦克斯韦最初设想的位移电流。 麦克斯韦没有对真空做任何特殊处理，把它当作一种物质介质。 对于麦克斯韦，P 的作用只是改变关系式 D = ε0εr E 中的相对介电常数 εr。

位移电流的现代合理性解释如下。

对于非常简单的介电材料，

• ε0，自由空间的介电常数，或电常数； 和
• εr，电介质的相对介电常数。

在上面的等式中，ε 的使用说明了介电材料的极化（如果有的话）。

位移电流的标量值也可以用电通量

标量 ε 的形式仅适用于线性各向同性材料。 对于线性非各向同性材料，ε 变为矩阵； 甚至更一般地，ε 可以用张量代替，张量可能取决于电场本身，或者可能表现出频率依赖性（因此产生色散）。