泊松方程

泊松方程是一个在理论物理学中具有广泛用途的椭圆偏微分方程。 例如，泊松方程的解是由给定电荷或质量密度分布引起的势场； 有了已知的势场，就可以计算出静电场或引力（力）场。 它是拉普拉斯方程的推广，在物理学中也经常出现。

泊松方法是 Δ φ = f {\displaystyle \Delta \varphi =f} 其中 Δ {\displaystyle \Delta } 是拉普拉斯算子，f {\displaystyle f} 和 φ {\displaystyle \varphi } 是流形上的实值或复值函数。 通常，给出 f {\displaystyle f} 并寻找 φ {\displaystyle \varphi }。 当流形为欧几里得空间时，拉普拉斯算子通常表示为 ∇2 因此泊松方程通常写为 ∇ 2 φ = f 。关于泊松方程的文章给出了泛松方程的格林函数的一般说明。 数值求解有多种方法，如松弛法、迭代算法等。

对于密度为 ρ 的大质量物体的引力场 g，利用微分形式的高斯引力定律可以得到相应的引力泊松方程 ∇ ⋅ g = − 4 π G ρ 。

如果质量密度为零，泊松方程简化为拉普拉斯方程。 相应的格林函数可用于计算距中心点质量 m 距离 r 处的势能（即基本解）。 在三维空间中，势能为 ϕ ( r ) = − G m r 。 {\displaystyle \phi (r)={\dfrac {-Gm}{r}}.} 相当于牛顿万有引力定律。

静电学的基石之一是建立和解决泊松方程描述的问题。 求解泊松方程相当于找到给定电荷分布 ρ f {\displaystyle \rho _{f}} 的电势 φ 。

静电学中泊松方程背后的数学细节如下（使用 SI 单位而不是电磁学中也经常使用的高斯单位）。

从微分形式的高斯电定律（也是麦克斯韦方程之一）开始，有 ∇ ⋅ D = ρ f {\displaystyle \mathbf {\nabla } \cdot \mathbf { D} =\rho _{f}} 其中 ∇ ⋅ {\displaystyle \mathbf {\nabla } \cdot } 是发散算子，D = 电位移场，ρf = 自由电荷体积密度（描述 从外面带来的费用）。

假设介质是线性、各向同性和均匀的（参见偏振密度），我们有本构方程，D = ε E {\displaystyle \mathbf {D} =\varepsilon \mathbf {E} } 其中 ε 是 介质的介电常数，E 是电场。

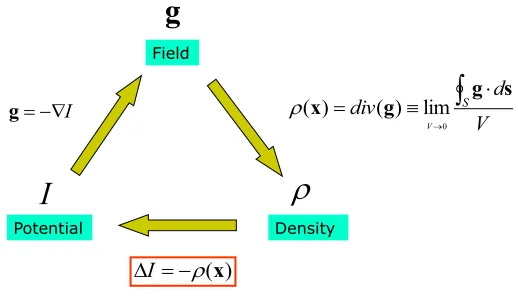
将其代入高斯定律并假设 ε 在感兴趣的区域中是空间常数，得到 ∇ ⋅ E = ρ ε 。 {\displaystyle \mathbf {\nabla } \cdot \mathbf {E} ={\frac {\rho }{\varepsilon }}~.} 其中 ρ {\displaystyle \rho } 是总体积电荷密度。 在静电学中，我们假设不存在磁场（以下论点在存在恒定磁场的情况下也成立）。 然后，我们有 ∇ × E = 0 , {\displaystyle \nabla \times \mathbf {E} =0,} 其中 ∇× 是卷曲运算符。 这个等式意味着我们可以将电场写成标量函数 φ（称为电势）的梯度，因为任何梯度的旋度都为零。 因此我们可以写，E = − ∇ φ , {\displaystyle \mathbf {E} =-\nabla \varphi ,} 其中引入了负号，因此 φ 被确定为每单位电荷的电势能 。