简介
编辑贝塞尔曲线 (/bɛz.i.eɪ/ BEH-zee-ay) 是一种用于计算机图形学和相关领域的参数化曲线。一组离散的控制点通过公式定义平滑、连续的曲线。 通常曲线旨在逼近真实世界的形状,否则没有数学表示或其表示未知或过于复杂。
贝塞尔曲线以法国工程师 Pierre Bézier(1910-1999 年)的名字命名,他在 1960 年代用它来设计雷诺汽车的车身曲线。其他用途包括计算机字体和动画的设计。
贝塞尔曲线可以组合形成贝塞尔样条,或推广到更高维度以形成贝塞尔曲面。贝塞尔三角形是后者的特例。
在矢量图形中,贝塞尔曲线用于模拟可以无限缩放的平滑曲线。路径,正如它们在图像处理程序中通常所指的那样,是链接的贝塞尔曲线的组合。路径不受光栅化图像的限制,修改起来很直观。
贝塞尔曲线也用于时域,特别是动画、用户界面设计和眼睛注视控制界面中的平滑光标轨迹。例如,贝塞尔曲线可用于指定对象随时间的速度,例如从 A 移动到 B 的图标,而不是简单地以每步固定的像素数移动。
当动画师或界面设计师谈论操作的物理原理或感觉时,他们可能指的是用于控制相关移动随时间变化的速度的特定贝塞尔曲线。
这也适用于机器人,例如,焊臂的运动应该平稳以避免不必要的磨损。
发明
编辑贝塞尔曲线的数学基础——伯恩斯坦多项式——建立于 1912 年,但多项式直到大约 50 年后才应用于图形,当时数学家 Paul de Casteljau 在 1959 年开发了 de Casteljau 算法,这是一种数值稳定的算法、评估曲线的方法,并成为第 一个将它们应用于法国汽车制造商雪铁龙计算机辅助设计的人。
具体案例
编辑贝塞尔曲线由一组控制点 P0 到 Pn 定义,其中 n 称为曲线的阶数(n = 1 表示线性,2 表示二次,3 表示三次,等等)。第 一个和最 后一个控制点始终是曲线的端点; 但是,中间控制点(如果有的话)通常不在曲线上。 以下部分中的总和应理解为仿射组合——即系数总和为 1。
线性贝塞尔曲线s
编辑给定不同的点 P0 和 P1,线性贝塞尔曲线只是这两点之间的一条线。
相当于线性插值。
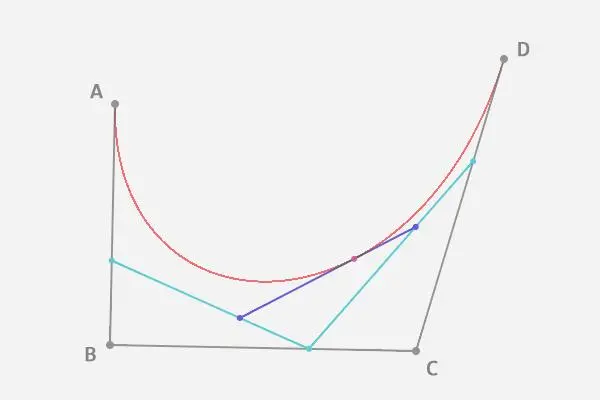
二次贝塞尔曲线s
编辑二次贝塞尔曲线是函数 B(t) 追踪的路径
可以理解为分别从P0到P1和从P1到P2的线性贝塞尔曲线上对应点的线性插值。
从中可以得出结论,曲线的切线在 P0 和 P2 处相交于 P1。当 t 从 0 增加到 1 时,曲线从 P0 沿 P1 的方向出发,然后从 P1 的方向弯曲到达 P2。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/194855/
