欧拉﹣伯努力栋梁方程

欧拉_伯努力梁方程（也称为工程师梁理论或经典梁理论）是线性弹性理论的简化，它提供了一种计算梁的承载和挠度特性的方法。 它涵盖了与仅承受横向载荷的梁的小挠度相对应的情况。 通过忽略剪切变形和旋转惯性的影响，它因此是 Timoshenko-Ehrenfest 梁理论的一个特例。 它大约在 1750 年首次被阐明，但直到 19 世纪后期埃菲尔铁塔和摩天轮的发展才得到大规模应用。 在这些成功的示范之后，它迅速成为工程学的基石和第二次工业xxx的推动者。

已经开发了其他数学模型，例如板理论，但梁理论的简单性使其成为科学中的重要工具，尤其是结构和机械工程。

曲线 w ( x ) {\displaystyle w(x)} 描述了光束在 z {\displaystyle z} 方向在某个位置 x {\displaystyle x} 的偏转（回想一下，光束被建模为 一维对象）。 q {\displaystyle q} 是分布载荷，换句话说是每单位长度的力（类似于压力是每面积的力）； 它可能是 x {\displaystyle x} 、 w {\displaystyle w} 或其他变量的函数。 E {\displaystyle E} 是弹性模量，而 I {\displaystyle I} 是梁截面的二次矩。 I {\displaystyle I} 必须相对于垂直于施加载荷并穿过横截面质心的轴进行计算。 明确地，对于轴沿 x {\displaystyle x} 并沿 z {\displaystyle z} 加载的梁，梁的横截面在 y z {\displaystyle yz} 平面中

通常，乘积 E I {\displaystyle EI}（称为抗弯刚度）是一个常数

该方程描述了均匀静态梁的偏转，在工程实践中得到广泛应用。 常见光束配置的偏转 w {\displaystyle w} 的表格表达式可以在工程手册中找到。

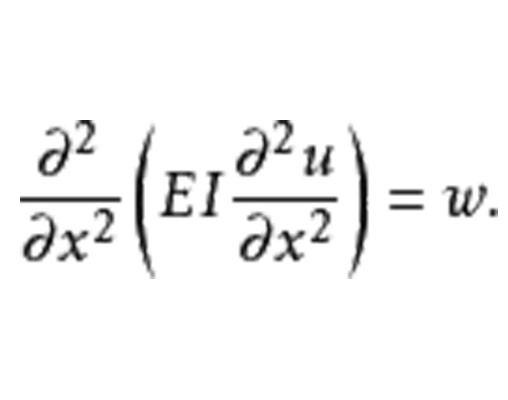
对于更复杂的情况，挠度可以通过直接积分法、麦考利法、矩面积法、共轭梁法、虚功原理、卡斯蒂利亚诺法等技术求解欧拉-伯努利方程来确定， 柔度法、坡度偏转法、力矩分配法或直接刚度法。

此处定义符号约定，因为可以在文献中找到不同的约定。 在本文中，使用右手坐标系，x {\displaystyle x} 轴在右，z {\displaystyle z} 轴指向上方，y {\displaystyle y} 轴指向 图。 当截面右侧与弯矩相关的扭矩矢量在正 y {\displaystyle y} 方向时，弯矩 M {\displaystyle M} 的符号取为正，即 M {\displaystyle M} 的正值会在底面产生压应力。