力矩

在物理学和力学中，扭矩是一个标准的机械量，是线性力的旋转当量。 它也称为力矩（也缩写为力矩）。 它表示力使身体的旋转运动发生变化的能力。 这个概念起源于阿基米德对xxx使用的研究，这反映在他的名言中：给我一个xxx和一个站立的地方，我将推动地球。 正如线性力是推力或拉力一样，扭矩可以被认为是物体绕特定轴的扭曲。 力矩被定义为力的垂直分量的大小与力的作用线与被确定的点之间的距离的乘积。 能量守恒定律也可以用来理解扭矩。 扭矩的符号通常是 τ {displaystyle {boldsymbol {tau }}} ，小写希腊字母 tau。 当称为力矩时，通常用M表示。

在三维空间中，力矩是一个伪向量； 对于点粒子，它由位置向量（距离向量）和力向量的叉积给出。 刚体扭矩的大小取决于三个量：施加的力、连接扭矩测量点和力施加点的xxx臂矢量，以及力和xxx臂矢量之间的角度。

• τ {displaystyle {boldsymbol {tau }}} 是扭矩矢量，τ {displaystyle tau } 是扭矩的大小，
• r {displaystyle mathbf {r} } 是位置向量（从测量扭矩的点到施加力的点的向量），
• F {displaystyle mathbf {F} } 是力向量，
• × {displaystyle times } 表示叉积，它根据右手法则产生垂直于 r 和 F 的向量，
• θ {displaystyle theta } 是力矢量与xxx臂矢量之间的夹角。

扭矩的 SI 单位是牛顿米 (N⋅m)。 有关扭矩单位的更多信息，请参阅§ 单位。

术语扭矩（从拉丁语 torquēre 到 twist）据说是由 James Thomson 提出并于 1884 年 4 月出版的。同年，Silvanus P. Thompson 在 Dynamo-Electric Machinery 的xxx版中证明了这一用法。 Thompson 对这个词的动机如下：

正如牛顿对力的定义是产生或倾向于产生运动（沿一条线）的力一样，扭矩可以定义为产生或倾向于产生扭转（绕轴）的力。 xxx使用一个将此动作视为单个确定实体的术语，而不是使用像 couple 和 moment 这样的术语，后者暗示了更复杂的想法。 应用扭转来转动轴的单一概念优于以一定xxx作用施加线性力（或一对力）的更复杂概念。

今天，根据地理位置和研究领域，扭矩被称为使用不同的词汇。 本文遵循美国物理学中使用的扭矩一词的定义。

在英国和美国的机械工程中，扭矩被称为力矩，通常简称为力矩。 至少从 1811 年起，Siméon Denis Poisson 在 Traité de mécanique 中就用法语证实了该术语。 该作品的英文译本于 1842 年问世。

垂直施加在xxx上的力乘以它到xxx支点的距离（xxx臂的长度）就是它的扭矩。 例如，在距支点两米处施加三牛顿的力与在距支点六米处施加一牛顿的力产生的扭矩相同。 力矩的方向可以用右手抓握定则来判断：如果右手的手指从xxx臂的方向向力的方向卷曲，则拇指指向力矩的方向。

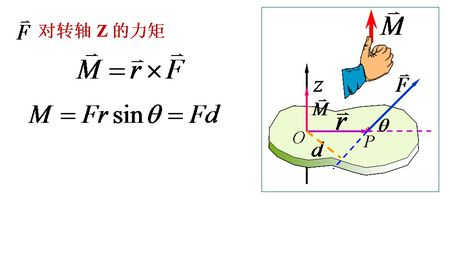
更一般地，点粒子（在某个参考系中具有位置 r）上的力矩可以定义为叉积

其中 F 是作用在粒子上的力。

其中 F 是施加的力的大小，θ 是位置和力向量之间的角度。

其中 F⊥ 是垂直于粒子位置的力的大小。