浮点数

在计算中，浮点算术 (FP) 是近似表示实数的算术，它使用具有固定精度的整数（称为有效数），按固定基数的整数指数缩放。 例如，12.345 可以表示为以 10 为底的浮点数：

实际上，大多数浮点系统使用以二为底数，但以十为底数（十进制浮点数）也很常见。

术语浮点数是指数字的小数点可以在数字的左、右或有效数字之间的任意位置浮动。 这个位置由指数表示，因此浮点数可以被认为是一种科学记数法。

浮点系统可以用来表示具有固定位数的数量级非常不同的数字——例如星系之间或原子中质子之间的米数。 出于这个原因，浮点运算通常用于允许需要快速处理时间的非常小和非常大的实数。 这种动态范围的结果是可以表示的数字不是均匀分布的； 两个连续可表示数字之间的差异随它们的指数而变化。

多年来，计算机中使用了多种浮点表示法。 1985 年，IEEE 754 浮点运算标准成立，自 1990 年代以来，最常遇到的表示是 IEEE 定义的表示。

浮点运算的速度（通常以 FLOPS 衡量）是计算机系统的一个重要特性，尤其是对于涉及密集数学计算的应用程序。

浮点单元（FPU，通俗地称为数学协处理器）是专门设计用于对浮点数执行运算的计算机系统的一部分。

数字表示指定了某种编码数字的方式，通常是一串数字。

数字串可以通过多种机制来表示数字。 在常用的数学符号中，数字串可以是任意长度，小数点的位置通过在此处放置一个明确的点字符（点或逗号）来指示。 如果未指定小数点，则该字符串隐式表示一个整数，未声明的小数点将位于字符串的右端，紧挨着最低有效位。 在定点系统中，字符串中的位置被指定为小数点。 因此，定点方案可能是使用中间有小数点的 8 位十进制数字的字符串，其中 00012345 表示 0001.2345。

在科学记数法中，给定数字按 10 的次方缩放，因此它位于某个范围内——通常在 1 到 10 之间，小数点紧接在xxx个数字之后。 比例因子为 10 的幂，然后在数字末尾单独指示。 例如，木星的卫星 Io 的轨道周期为 152,853.5047 秒，这个值可以用标准形式的科学记数法表示为 1.528535047×105 秒。

浮点表示在概念上类似于科学记数法。 从逻辑上讲，浮点数包括：

• 在给定基数（或基数）中给定长度的带符号（表示正数或负数）数字串。 此数字串称为尾数、尾数或系数。 有效数字的长度决定了可以表示数字的精度。 假定小数点位置始终位于有效数内的某个位置——通常恰好在最高有效数字之后或之前，或者在最右边（最低有效）数字的右侧。 本文一般遵循小数点设置在最重要（最左边）数字之后的约定。
• 一个带符号的整数指数（也称为特征或尺度），它修改数字的大小。

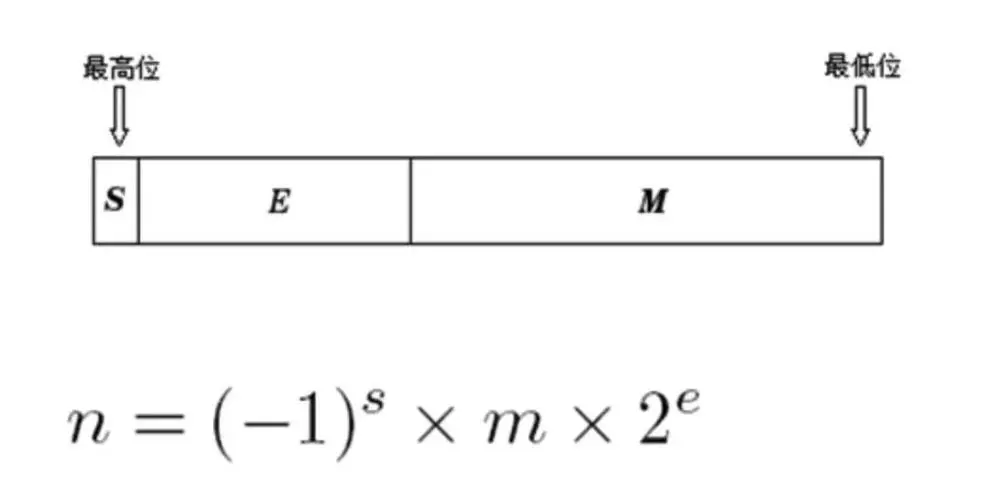
为了导出浮点数的值，将有效数乘以基数的指数次方，相当于将小数点从其隐含位置移动等于指数值的位数——到 如果指数为正，则在右侧；如果指数为负，则在左侧。

以 10 进制（熟悉的十进制表示法）为例，具有十位精度的数字 152,853.5047 表示为有效数字 1,528,535,047 和指数 5。 为确定实际值，小数点放在尾数的xxx位后，结果乘以 105 得到 1.528535047×105，即 152,853.5