超二次曲面体

在数学中，超二次曲面或超二次曲面（也称为超二次曲面）是一组由类似于椭圆体和其他二次曲面的公式定义的几何形状，只是平方运算被任意幂代替。 它们可以看作是超椭圆的三维亲戚。 根据上下文，该术语可能指固体物体或其表面。 下面的方程式指定了表面； 通过用小于或等于符号替换等号来指定实体。

超二次曲面包括许多类似立方体、八面体、圆柱体、菱形和纺锤体的形状，带有圆角或尖角。 由于它们的灵活性和相对简单性，它们是流行的几何建模工具，尤其是在计算机图形学中。

一些作者，例如 Alan Barr，将超二次曲面定义为包括超椭圆体和超环面。 然而，（适当的）超环面不是上面定义的超二次曲面； 并且，虽然一些超二次曲面是超椭圆体，但两个家族都不包含在另一个家族中。专着涵盖了超二次曲面的几何特性及其从距离图像中恢复的方法的全面覆盖。

其中 r、s 和 t 是确定超二次曲面主要特征的正实数。 即：

• 小于 1：修改为具有凹面和锐边的尖八面体。
• 正好是 1：一个正八面体。
• 介于 1 和 2 之间：修改为具有凸面、钝边和钝角的八面体。
• 恰好 2：一个球体
• 大于 2：修改为具有圆形边角的立方体。
• 无限（在极限内）：一个立方体

每个指数可以独立变化以获得组合形状。 例如，如果r=s=2，t=4，则得到一个旋转体，它类似于具有圆形横截面但两端扁平的椭圆体。 当（且仅当）r = s 时，此公式是超椭球公式的特例。

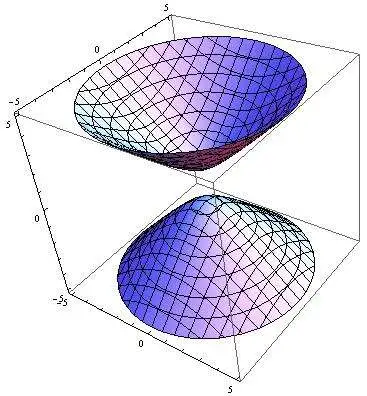
如果允许任何指数为负，则形状会延伸到无穷大。 这种形状有时被称为超双曲面。

上面的基本形状沿每个坐标轴从 -1 跨越到 +1。 一般超二次曲面是将此基本形状沿每个轴按不同量 A、B、C 缩放的结果。

表面参数 u 和 v（如果 m 等于 2，则相当于经度和纬度）的参数方程