计算理论
编辑在理论计算机科学和数学中,计算理论是处理在计算模型上可以解决哪些问题、使用算法、解决这些问题的效率或程度(例如,近似解决方案与精确解决方案)的分支 ). 该领域分为三个主要分支:自动机理论和形式语言、可计算性理论和计算复杂性理论,它们由以下问题联系起来:计算机的基本能力和局限性是什么?。
为了对计算进行严格的研究,计算机科学家使用计算机的数学抽象,称为计算模型。 有几种模型在使用,但最常检查的是图灵机。 计算机科学家研究图灵机是因为它易于表述,可以分析并用于证明结果,还因为它代表了许多人认为最强大的合理计算模型(参见丘奇-图灵论文)。 潜在的无限内存容量似乎是一个无法实现的属性,但图灵机解决的任何可判定问题总是只需要有限数量的内存。 所以原则上,任何可以由图灵机解决(决定)的问题都可以由具有有限内存的计算机解决。
历史
编辑计算理论可以被认为是计算机科学领域中各种模型的创建。 因此,使用数学和逻辑。 上个世纪它成为一门独立的学科,与数学分离。
计算理论的一些先驱是拉蒙·鲁尔、阿朗佐·丘奇、库尔特·哥德尔、艾伦·图灵、斯蒂芬·克莱恩、罗萨·彼得、约翰·冯·诺依曼和克劳德·香农。
分支机构
编辑自动机理论
编辑自动机理论是对抽象机器(或更恰当地说,抽象“数学”机器或系统)以及可以使用这些机器解决的计算问题的研究。 这些抽象机器称为自动机。 Automata 来自希腊语单词 (Αυτόματα),意思是某物正在自己做某事。自动机理论也与形式语言理论密切相关,因为自动机通常按它们能够识别的形式语言类别进行分类。 自动机可以是形式语言的有限表示,而形式语言可能是无限集。 自动机用作计算机器的理论模型,并用于证明可计算性。
形式语言理论
语言理论是数学的一个分支,它关注将语言描述为对字母表的一组操作。 它与自动机理论密切相关,因为自动机用于生成和识别形式语言。 有几类形式语言,每一种都允许比之前的更复杂的语言规范,即乔姆斯基层次结构,每一种都对应于一类识别它的自动机。 因为自动机被用作计算模型,所以形式语言是任何必须计算的问题的首选规范模式。
可计算性理论
编辑可计算性理论主要处理问题在计算机上可解决的程度的问题。 图灵机无法解决停机问题是可计算性理论中最重要的成果之一,因为它是一个具体问题的示例,该问题既易于表述又无法使用图灵机解决。 许多可计算性理论都建立在停机问题的结果之上。
可计算性理论的另一个重要步骤是赖斯定理,该定理指出对于偏函数的所有非平凡属性,图灵机是否计算具有该属性的偏函数是不可判定的。
可计算性理论与称为递归理论的数理逻辑分支密切相关,递归理论消除了仅研究可简化为图灵模型的计算模型的限制。 许多研究递归理论的数学家和计算理论家将其称为可计算性理论。
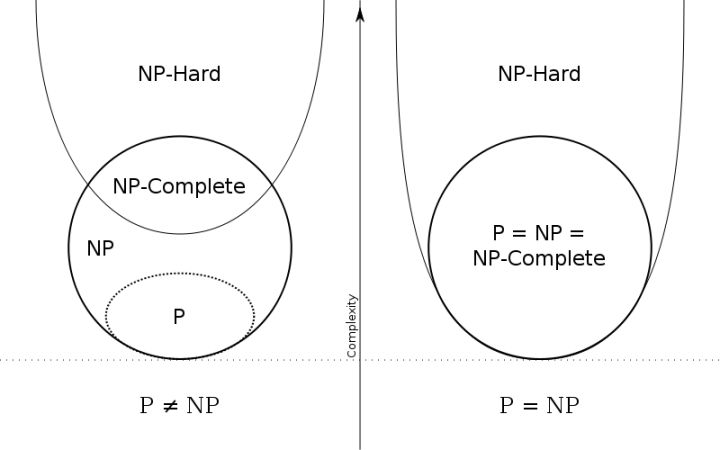
计算复杂性理论
编辑复杂性理论不仅考虑一个问题是否可以在计算机上完全解决,而且还考虑解决问题的效率。 主要考虑两个方面:时间复杂度和空间复杂度,分别是执行一次计算需要多少步,以及执行该计算需要多少内存。
为了分析给定算法需要多少时间和空间,计算机科学家将解决问题所需的时间或空间表示为输入问题大小的函数。 例如,随着数字列表变大,在一长串数字中查找特定数字会变得更加困难。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/198218/
