科里奥利频率

科里奥利频率 ƒ，也称为科里奥利参数或科里奥利系数，等于地球自转速率 Ω 的两倍乘以纬度 φ  的正弦值。

f = 2 Ω sin ⁡ φ 。

地球的自转速率 (Ω = 7.2921 × 10−5 rad/s) 可以计算为每秒 2π / T 弧度，其中 T 是地球的自转周期，即一个恒星日（23 小时 56 分 4.1 秒） ). 在中纬度地区，f {\displaystyle f} 的典型值约为 10−4 rad/s。 地球表面的惯性振荡具有这个频率。 这些振荡是科里奥利效应的结果。

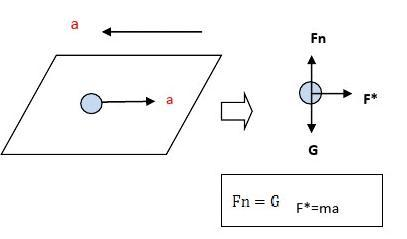
考虑一个物体（例如固定体积的大气）在地球旋转参考系中以速度 v 沿给定纬度 φ 移动。 在身体的局部参考系中，垂直方向平行于从地球中心指向身体所在位置的径向矢量，水平方向垂直于该垂直方向并在子午方向上。 因此，科里奥利力总是与局部垂直方向成角度 φ {。 因此，科里奥利力的局部水平方向为 Ω sin ⁡ φ 。 该力用于沿经度或子午线方向移动身体。

假设物体以速度 v 移动，使得向心力和科里奥利力在其上的力是平衡的。 然后我们有

v 2 / r = 2 ( Ω sin ⁡ φ ) v

其中 r {\displaystyle r} 是物体路径的曲率半径（由 v {\displaystyle v} 定义）。 替换 v = r ω ，其中 ω 是地球自转速率的大小，我们得到

f = ω = 2 Ω sin ⁡ φ 。

因此，科里奥利参数 f 是将物体保持在固定的纬度圈或带状区域所需的角速度或频率。 如果科里奥利参数很大，地球自转对身体的影响就很大，因为它需要更大的角频率才能与科里奥利力保持平衡。 或者，如果科里奥利参数很小，地球自转的影响也很小，因为只有一小部分作用在身体上的向心力被科里奥利力抵消了。 因此，f 的大小强烈影响有助于身体运动的相关动力学。 这些考虑因素体现在无量纲化罗斯贝数中。

在稳定性计算中，f 沿子午线方向的变化率变得很重要。 这称为 Rossby 参数，通常表示为

β = ∂ f ∂ y ，其中 y 是增加子午线的局部方向。 这个参数变得很重要，例如，在涉及罗斯贝波的计算中。