谐振子

在经典力学中，谐振子是一个系统，当它从平衡位置发生位移时，会受到与位移 x 成正比的恢复力 F：F → = − k x → , 其中 k 是正常数。

如果 F 是作用在系统上的xxx力，则系统称为简谐振子，它进行简谐振动：关于平衡点的正弦振荡，具有恒定的振幅和恒定的频率（不依赖于振幅 ).

如果还存在与速度成正比的摩擦力（阻尼），则谐振子被描述为阻尼振荡器。 根据摩擦系数，系统可以：

• 以低于无阻尼情况下的频率振荡，并且振幅随时间减小（欠阻尼振荡器）。
• 衰减到平衡位置，没有振荡（过阻尼振荡器）。

欠阻尼振荡器和过阻尼振荡器之间的边界解出现在特定的摩擦系数值处，称为临界阻尼。

如果存在外部时间相关力，则谐波振荡器被描述为驱动振荡器。

机械示例包括摆（具有小位移角度）、连接到弹簧的质量和声学系统。 其他类似系统包括电谐波振荡器，例如 RLC 电路。 谐振子模型在物理学中非常重要，因为任何质量在稳定平衡中受到力的作用都作为微小振动的谐振子。 谐振子在自然界中广泛存在，并在许多人造设备中得到利用，例如时钟和无线电电路。 它们几乎是所有正弦振动和波的来源。

简谐振子

简谐振子是一种既没有驱动也没有阻尼的振荡器。 它由质量 m 组成，该质量受到单个力 F，该力将质量拉向点 x = 0 的方向，并且仅取决于质量的位置 x 和常数 k。 系统的力平衡（牛顿第二定律）为 F = m a = m d 2 x d t 2 = m x ¨ = − k x 。

求解这个微分方程，我们发现运动由函数 x ( t ) = A cos ⁡ ( ω t + φ ) ,

运动是周期性的，以恒定振幅 A 以正弦方式重复自身。除了振幅之外，简谐振子的运动的特征在于其周期 T = 2 π / ω ，单次振荡的时间或其频率 f = 1 / T ，单位时间内的周期数。 给定时间 t 的位置还取决于相位 φ，它决定了正弦波的起点。 周期和频率由质量 m 的大小和力常数 k 决定，而幅度和相位由起始位置和速度决定。

简谐振子的速度和加速度以与位置相同的频率振荡，但相位不同。 零位移时速度xxx，而加速度的方向与位移相反。

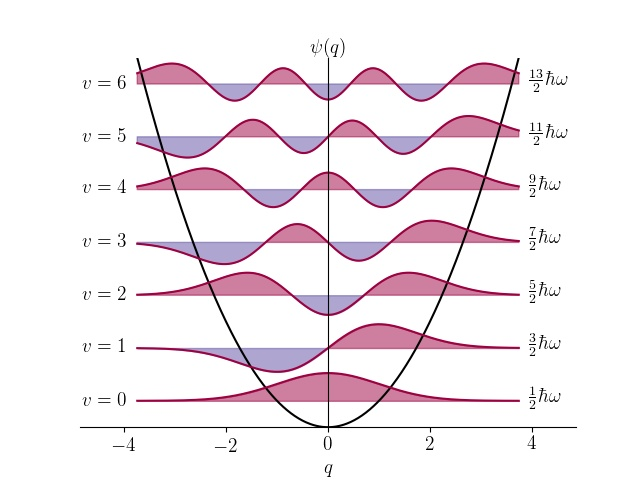
在位置 x 处存储在简谐振子中的势能是 U = 1 2 k x 2 。

阻尼谐振子

在真实的振荡器中，摩擦或阻尼会减慢系统的运动。 由于摩擦力，速度与作用的摩擦力成比例地减小。 在简单的无驱动谐振子中，作用在质量上的xxx力是恢复力，而在阻尼谐振子中，另外还有一个摩擦力，该摩擦力始终与运动相反。 在许多振动系统中，摩擦力 Ff 可以建模为与物体的速度 v 成正比：Ff = −cv，其中 c 称为粘性阻尼系数。